Katy MO
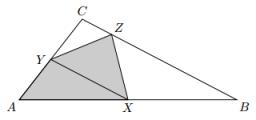
Kate drew a triangle ABC. The middle of the line segment AB is marked as X, and the center of the side AC is marked as Y. On the side BC, she wants to find point Z so that the area of a 4gon AXZY is the greatest. What part of the ABC triangle can maximally occupy 4-gon AXZY?
Final Answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
planimetricsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Triangle ABC
There is the triangle ABC with the side BC of length 2 cm. Point K is the middle point of AB. Points L and M split the AC side into three equal lines. KLM is an isosceles triangle with a right angle at point K. Determine the lengths of the sides AB, AC tr - Equilateral triangle ABC
In the equilateral triangle ABC, K is the center of the AB side, the L point lies on one-third of the BC side near point C, and point M lies on one-third of the side of the AC side closer to point A. Find what part of the ABC triangle contains the triangl - MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Grassland and goat
An unfenced grassland is a right triangle ABC with AB = 4m, BC = 8m, and AC as hypotenuse. A goat is tied to a 5-m long rope with its stake at point O, which is 2m from side AB and 2m from the prolongation of side BC through corner B. Then: 1. How far is - Applies 14683
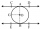Point B is the center of the circle. The line AC touches the circles at point C and applies AB = 20 cm and AC = 16 cm. What is the radius of the circle BC? - Ratio of triangles areas
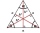In an equilateral triangle ABC, the point T is its center of gravity, the point R is the image of the point T in axial symmetry along the line AB, and the point N is the image of the point T in axial symmetry along the line BC. Find the ratio of the areas - Maturitný - RR - base
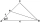In an isosceles triangle ABC with base AB, ∠BAC = 20°, AB = 4. The axis of the interior angle at vertex B intersects side AC at point P. Calculate the length of the segment AP. Give the result to two decimal places.
