Výslednice 3
Na hmotný bod působí dvě stejné síly o velikosti 30 N. Urči velikost výslednice, svírají-li tyto síly úhel 42°.
Vaše odpověď:
Vaše odpověď:
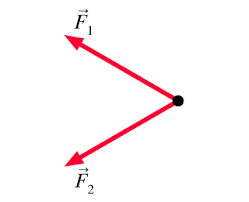
Zobrazuji 1 komentář:
Dr Math
Reseni jako scitani vektoru - https://www.hackmath.net/cz/kalkulacka/soucet-vektoru?a=30&a1=42&b=30&submit=Vy%C5%99e%C5%A1
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetrieJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Na hmotný
Na hmotný bod M působí síly F1, F2 o velikosti 40 N. Jejich výslednice má velikost 60 N. Určete úhel, který síly F1 a F2 svírají. - Vektorový součet sil
Síly o velikostech F1 = 42 N a F2 = 35 N působí ve společném bodě a svírají úhel o velikosti 77°12´. Jak veliká je jejich výslednice? - Dvě síly
Dvě síly s velikostí 25 a 30 Newtonův působí na objekt v úhlech 10° a 100°. Najděte směr a velikost výsledné síly. Zaokrouhlete na dvě desetinná místa mezivýpočty a konečnou odpověď. - Jsou podobné
Trojúhelníky ABC a A'B'C 'jsou podobné s koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou alfa = 35°, beta = 48°. Urči velikosti všech úhlů trojúhelníku A'B'C '. - Koeficient podobnosti
Trojúhelníky ABC a A "B" C "jsou podobné koeficientem podobnosti 2. Velikosti úhlů trojúhelníku ABC jsou α = 35° a β = 48°. Urči velikosti všech úhlů trojúhelníku A" B "C". - Úhel mezi silami
V jednom bodě působí dvě síly o velikosti 8 Newtonů a 15 Newtonů. Pokud je výsledná síla 17 Newtonů, najděte úhel mezi silami. - Tři síly - vektory
Tři síly, jejichž velikosti jsou v poměru 9:10:17, působí v rovině v jednom bodě tak, že jsou v rovnováze. Určete velikosti úhlů, které svírají každé dvě síly
