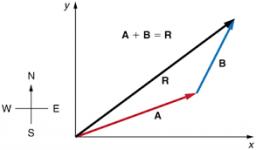
Vektorový součet sil

Síly o velikostech F1 = 42N a F2 = 35N působí ve společném bodě a svírají úhel o velikosti 77°12´. Jak veliká je jejich výslednice?

Správná odpověď:

F =  60,3353 N

Postup správného řešení:

F1​=42 N F2​=35 N α=77°12′=77°+6012​°=77,2°=77,2  x0​=F1​=42 y0​=0 x=x0​+F2​⋅ cosα=x0​+F2​⋅ cos77,2° =42+35⋅ cos77,2° =42+35⋅ 0,221548=49,7542 y=y0​+F2​⋅ sinα=y0​+F2​⋅ sin77,2° =0+35⋅ sin77,2° =0+35⋅ 0,975149=34,13023 F=x2+y2​=49,75422+34,13022​=60,3353 N

Zkusit jiný příklad


Našel jsi chybu či nepřesnost? Klidně nám ji napiš.







Tipy na související online kalkulačky
Potřebujete pomoci spočítat smíšená čísla? Zkuste naši kalkulačku na smíšená čísla.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.

K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:

geometriearitmetikaplanimetriečíslagoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu

 
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1

Související a podobné příklady: