Z8–I–5 MO 2019
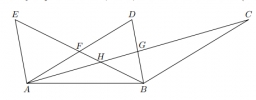
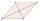
Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm2 a obsah čtyřúhelníku DFHG je 8 cm2
Určete obsahy trojúhelníků AFE, AHF, ABG a BGH.
Vaše odpověď:
Určete obsahy trojúhelníků AFE, AHF, ABG a BGH.
Vaše odpověď:
Zobrazuji 4 komentáře:
Matematik
protože nezáleží, jak daleko je ten bod, když je výška stejná protože S= av/2 a S(ABF) = S(ABG), takže to je stejný
Tipy na související online kalkulačky
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetriezákladní operace a pojmytémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Narýsuj 4
Narýsuj do jednoho obrazku : a) přímku RZ b) YZ, pro kterou platí YZ je kolmá k RZ c) polopřímku RS různoběžnou s YZ i s přímkou RZ d) bod F, který leží na YZ mimo již zvolené body e) bod H, který leží na polopřímce RS i přímce RZ - Body v rovině
V rovině je dáno 12 bodů, z nichž 5 leží na jedné přímce. Kolik různých přímek určují dané body? - Trojúhelník
V trojúhelníku ABC se stranou BC délky 2 cm je bod K středem strany AB. Body L a M rozdělují stranu AC na tři shodné úsečky. Trojúhelník KLM je rovnoramenný s pravým úhlem u vrcholu K. Určete délky stran AB, AC trojúhelníku ABC. - MO - trojúhelníky
Na stranách AB a AC trojúhelníku ABC lěží po řadě body E a F, na úsečce EF leží bod D. Přmky EF a BC jsou rovnoběžné a součastně platí FD : DE = AE : EB = 2:1. Trojúhelník ABC má obsah 27 hektarů a úsečkami EF, AD a DB je rozdělen na čtyři části . Určete - Sestrojte
Sestrojte kosočtverec ABCD, pokud velikost úhlopříčky AC je 6 cm a BD je 8 cm. - Délka úsečky EF
Čtyřúhelník ABCD je souměrný podle úhlopříčky AC. Délka AC je 12 cm, délka BC je 6 cm a vnitřní úhel u vrcholu B je pravý. na stranách AB, AD jsou dány body E, F tak, že trojúhelník ECF je rovnostranný. Určete délku úsečky EF. - V rovině 2
V rovině je umístěn trojúhelník ABC s pravým úhlem u vrcholu C, pro který platí: A(1, 2), B(5, 2), C(x, x+1), kde x > -1. a) určete hodnotu x b) určete souřadnice bodu M, který je středem úsečky AB c) dokažte že vektory AB a CM jsou kolmé d) určete vel
