Z8–I–5 MO 2019
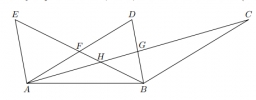
For eight different points as shown in the figure, points C, D, and E lie on a line parallel to line AB, F is the midpoint of line AD, G is the midpoint of line AC, and H is the intersection of lines AC and BE. The area of triangle BCG is 12 cm2 and the area of quadrilateral DFHG is 8 cm2
Determine the areas of triangles AFE, AHF, ABG, and BGH.
Determine the areas of triangles AFE, AHF, ABG, and BGH.
Final Answer:
Tips for related online calculators
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticplanimetricsbasic operations and conceptsthemes, topicsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- MO - triangles
On the AB and AC sides of the ABC triangle lies successive points E and F, and on segment EF lie point D. The EF and BC lines are parallel. It is true this ratio FD:DE = AE:EB = 2:1. The area of the ABC triangle is 27 hectares, and line segments EF, AD, a - Area of triangle
Two pairs of parallel lines, AB to CD and AC to BD, are given. Point E lies on the line BD, point F is the midpoint of the segment BD, point G is the midpoint of the segment CD, and the area of the triangle ACE is 20 cm². Determine the area of triangl - Line segments
Triangle ABC is divided by line segments. Lines DE and AB are parallel. Two lines are drawn from vertex C. The first line intersects points H and F on segments DE and AB. The second line intersects points I and G on segments DE and AB. Triangles CDH, CHI, - Triangle angle operations
There are also two equilateral triangles ABC, and BDE, such that the size of the angle ABD is greater than 120° and less than 180° points C and E lie in the same half-plane defined by the line AD. The intersection of CD and AE is marked F. Determine the s - Angle of two lines
There is a regular quadrangular pyramid ABCDV; | AB | = 4 cm; height v = 6 cm. Determine the angles of lines AD and BV. - Quadrilateral triangle segment
The quadrilateral ABCD is symmetrical about the diagonal AC. The length of AC is 12 cm, the length of BC is 6 cm, and the interior angle at vertex B is right. points E and F are given on the sides AB, and AD so that the triangle ECF is equilateral. Determ - There
There is a triangle ABC: A (-2,3), B (4, -1), C (2,5). Determine the general equations of the lines on which they lie: a) AB side, b) height to side c, c) Axis of the AB side, d) median ta to side a
