MO - trojúhelníky
Na stranách AB a AC trojúhelníku ABC lěží po řadě body E a F, na úsečce EF leží bod D. Přmky EF a BC jsou rovnoběžné a součastně platí FD : DE = AE : EB = 2:1. Trojúhelník ABC má obsah 27 hektarů a úsečkami EF, AD a DB je rozdělen na čtyři části . Určete obsahy těchto čtyř částí.
Správná odpověď:
Zobrazuji 3 komentáře:
Ries.mr
Nápověda. Začněte s obsahem trojúhelníku AEF.
Přímky EF a BC jsou rovnoběžné, souhlasné úhly u vrcholů E a B, resp. u vrcholů F a C jsou shodné, trojúhelníky AEF a ABC jsou tudíž podobné. Odpovídající koeficient podobnosti je roven:
|AE| : |AB| = |AE| : (|AE| + |EB|) = 2:3
Obsahy těchto trojúhelníků jsou proto v poměru AEF : ABC =4:9
takže AEF = ABC · 4 : 9 = 12 hektarů;
Úsečka AD dělí trojúhelník AEF na dva trojúhelníky, jejichž obsahy jsou ve stejném poměru jako délky úseček FD a DE, tedy
ADF : ADE = |FD| : |DE| =2:1
Odtud plyne, že ADE = AEF : 3 = 4 hektary a ADF = 2 · ADE = 8 hektarů. Úsečka DE dělí trojúhelník ABD na dva trojúhelníky, jejichž obsahy jsou ve stejném poměru jako délky úseček AE a EB, tedy
ADE : BDE = |AE| : |EB| =2:1
Odtud plyne, že BDE = ADE : 2 = 2 hektary
Nyní známe obsahy tří ze čtyř částí trojúhelníku ABC, obsah té poslední je roven rozdílu BCFD = ABC − AEF − BDE = 13 hektarů. Obsahy částí trojúhelníku ABC v hektarech jsou:
BED = 2, AED = 4, ADF = 8, BCFD = 13
Přímky EF a BC jsou rovnoběžné, souhlasné úhly u vrcholů E a B, resp. u vrcholů F a C jsou shodné, trojúhelníky AEF a ABC jsou tudíž podobné. Odpovídající koeficient podobnosti je roven:
|AE| : |AB| = |AE| : (|AE| + |EB|) = 2:3
Obsahy těchto trojúhelníků jsou proto v poměru AEF : ABC =4:9
takže AEF = ABC · 4 : 9 = 12 hektarů;
Úsečka AD dělí trojúhelník AEF na dva trojúhelníky, jejichž obsahy jsou ve stejném poměru jako délky úseček FD a DE, tedy
ADF : ADE = |FD| : |DE| =2:1
Odtud plyne, že ADE = AEF : 3 = 4 hektary a ADF = 2 · ADE = 8 hektarů. Úsečka DE dělí trojúhelník ABD na dva trojúhelníky, jejichž obsahy jsou ve stejném poměru jako délky úseček AE a EB, tedy
ADE : BDE = |AE| : |EB| =2:1
Odtud plyne, že BDE = ADE : 2 = 2 hektary
Nyní známe obsahy tří ze čtyř částí trojúhelníku ABC, obsah té poslední je roven rozdílu BCFD = ABC − AEF − BDE = 13 hektarů. Obsahy částí trojúhelníku ABC v hektarech jsou:
BED = 2, AED = 4, ADF = 8, BCFD = 13
9 let 1 Like
Žák
Myslim ze ak strany podobnych trojuhelniku jsou v pomeru 2:3 tak obsahy jsou v druhe mocnine teda 4:9
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Chcete proměnit jednotky času, např. hodiny na minuty?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometrieplanimetriezákladní operace a pojmyJednotky fyzikálních veličintémaÚroveň náročnosti úkolu
Související a podobné příklady:
- Rovnostranný 81097
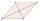Čtyřúhelník ABCD je souměrný podle úhlopříčky AC. Délka AC je 12 cm, délka BC je 6 cm a vnitřní úhel u vrcholu B je pravý. na stranách AB, AD jsou dány body E, F tak, že trojúhelník ECF je rovnostranný. Určete délku úsečky EF. - Z8–I–5 MO 2019
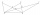Pro osm navzájem různých bodů jako na obrázku platí, že body C, D, E leží na přímce rovnoběžné s přímkou AB, F je středem úsečky AD, G je středem úsečky AC a H je průsečíkem přímek AC a BE. Obsah trojúhelníku BCG je 12 cm² a obsah čtyřúhelníku DFHG je 8 c - MO Z9 2019 domace kolo
V trojúhelníku ABC leží bod P ve třetině úsečky AB blíže bodu A, bod R je ve třetině úsečky P B blíže bodu P a bod Q leží na úsečce BC tak, že úhly P CB a RQB jsou shodné. Určete poměr obsahů trojúhelníků ABC a PQC. - Z7–I–5 MO 2022
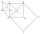Na obrázku jsou znázorněny čtverce ABCD, EFCA, CHCE a IJHE. Body S, B, F a G jsou po řadě středy těchto čtverců. Úsečka AC je dlouhá 1 cm. Určete obsah trojúhelníku IJS. Prosím pomozte... - Čtyřúhulník AFHD
Trojúhelník ABC je rozdělen úsečkami. Úsečky DE a AB jsou rovnoběžné. Trojúhelníky CDH, CHI, CIE, FIH mají stejný obsah a to 8 dm². Zjistěte obsah čtyřúhelníku AFHD. - Lichoběžník 21
Je dán lichoběžníku ABCD s rovnoběžnými stranami AB a CD pro bod E strany AB plati, že úsečka DE dělí lichoběžník na dvě části se stejným obsahem. Spočítej délku úsečky AE. - Kolineární 83065
Body A, B a C jsou kolineární a B leží mezi A a C. Pokud AC = 48, AB = 2x + 2 a BC = 3x + 6, jaká je délka BC?
