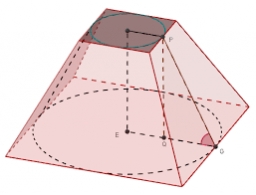
Digging a pit
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14 m and 10 m long. The sidewalls form an angle of 135° with a smaller base. Find how many m3 of soil were excavated when digging the pit.
Your answer:
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Pyramid soil
The pit is a regular truncated 4-sided pyramid, with 14 m and 10 m base edges and a depth of 6 m. Calculate how much m³ of soil was removed when we dug this pit. - Tetrahedral pyramid 8
Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - Pyramid edge calculation
The foundations of a regular truncated quadrilateral pyramid are squares. The lengths of the sides differ by 6 dm. Body height is 7 dm. The body volume is 1813 dm³. Calculate the lengths of the edges of both bases. - Pyramid measurements
Calculate the surface area and volume of a regular quadrilateral truncated pyramid if the base edges are 87 cm and 64 cm and the wall height is 49 cm. - 4B - truncated pyramid
Calculate the volume of a regular truncated quadrilateral pyramid if the base edges are 10 cm and 4 cm and the slant height of the lateral face is 5 cm. - Pillar
Calculate the volume of a pillar in the shape of a regular quadrilateral frustum (truncated pyramid) with base edges a = 10 and b = 19, and height h = 28. - Truncated pyramid
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
