Tetrahedral pyramid 8
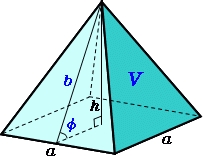
Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h=100.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Digging a pit
The pit has the shape of a regular quadrilateral truncated pyramid. The edges of the bases are 14 m and 10 m long. The sidewalls form an angle of 135° with a smaller base. Find how many m³ of soil were excavated when digging the pit. - Tetrahedral pyramid
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Octagonal pyramid
Find the volume of a regular octagonal pyramid with height v = 100 and the angle of the side edge with the base plane is α = 60°. - Tetrahedral pyramid
Calculate the regular tetrahedral pyramid's volume and surface if the area of the base is 20 cm² and the deviation angle of the side edges from the plane of the base is 60 degrees. - Distance of points
A regular quadrilateral pyramid ABCDV is given, in which edge AB = a = 4 cm and height v = 8 cm. Let S be the center of the CV. Find the distance of points A and S. - Tetrahedral pyramid
It is given a regular tetrahedral pyramid with a base edge of 6 cm and a height of pyramid 10 cm. Calculate the length of its side edges. - Pyramid
The pyramid has a base a = 2cm and height in v = 7 cm. a) calculate the angle between plane ABV and the base plane b) Calculate the angle between the edges on the opposite side.
