Cotangent - practice problems
In a right triangle, the cotangent is defined as the ratio of the adjacent perpendicular to the opposite perpendicular. It is the reciprocal value of the tangent of a given angle.Direction: Solve each problem carefully and show your solution in each item.
Number of problems found: 37
- One side 4
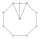One side of a regular octagon is 12 inches. Find the apothem and its area. - Apex of the Isosceles triangle
The angle at the apex of an isosceles triangle is 78°. The base is 28.5cm long. What is the shoulder length? - A hiker
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - Cross-section - trapezoid
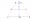The cross-section of the channel has the shape of a trapezoid. The bottom width is 2.25 m, and the depth is 5 m. The walls have a slope of 68°12' and 73°45'. Calculate the upper channel width. - Three pillars
On a straight road, three pillars are 6 m high at the same distance of 10 m. At what angle of view does Vlado see each pillar if it is 30 m from the first and his eyes are 1.8 m high? - Powerplant chimney
From the building window at the height of 7.5 m, we can see the top of the factory chimney at an altitude angle of 76° 30 ′. We can see the chimney base from the same place at a 5° 50 ′ depth angle. How tall is the chimney? - Traffic sign
There is a traffic sign for climbing on the road with an angle of 7%. Calculate at what angle the road rises (falls). - Fighter
A military fighter flies at an altitude of 10 km. The ground position was aimed at an altitude angle of 23° and 12 seconds later at an altitude angle of 27°. Calculate the speed of the fighter in km/h. - TV tower
Calculate the height of the television tower if an observer standing 430 m from the base of the tower sees the peak at an altitude angle of 23°. - The ladder
The ladder touches a wall at the height of 7.5 m. The angle of the inclination of the ladder is 76°. How far is the lower end of the ladder from the wall? - Observation tower
The observation tower has a height of 105 m above sea level. The ship is aimed at a depth angle of 1° 49' from the tower. How far is the ship from the base of the tower? - The rescue helicopter
The rescue helicopter is above the landing site at a height of 180m. The rescue operation site can be seen from here at a depth angle of 52°40'. How far will the helicopter land from the rescue site? - Perpendicular line
According to the map, the scouts were supposed to proceed through the forest perpendicular to its straight edge, where the goal was 3 km away from the starting point. They already deviated from the correct direction by 5° at the start. How far from the ta - Tetrahedral pyramid 8
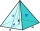Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=40° B=70° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - A drone
A flying drone aimed the area for an architect. He took off perpendicularly from point C to point D. He was 300 m above ABC's plane. The drone from point D pointed at a BDC angle of 43°. Calculate the distance between points C and B in meters. - Cone side
Calculate the volume and area of the cone whose height is 10 cm, and the axial section of the cone has an angle of 30 degrees between height and the cone side. - Tetrahedral pyramid
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'. - Heptagonal pyramid
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Depth angles
At the top of the mountain stands a castle with a tower 30 meters high. We see the crossroad at a depth angle of 32°50' and the heel at 30°10' from the top of the tower. How high is the top of the mountain above the crossroad? - Calculate sides
In the triangle, the side length AB = 6 cm, the height to side c = 5 cm, and the angle BCA = 35°. Calculate sides a b.
Do you have unsolved math question and you need help? Ask a question, and we will try to solve it. We solve math question.
