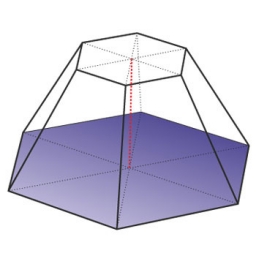
Heptagonal pyramid
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm3.
Correct answer:
Showing 1 comment:
Math student
Problem #1] The aluminum frustum of a right circular cone has an altitude of 15 inches and, whose upper and lower bases have a radii 10 inches and 5 inches respectively; find the following;
a) The lateral surface area in ft2 .
b) The total surface area in ft2 .
c) The volume of the frustum of the cone in ft3 .
a) The lateral surface area in ft2 .
b) The total surface area in ft2 .
c) The volume of the frustum of the cone in ft3 .
Tips for related online calculators
Looking for a statistical calculator?
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you know the volume and unit volume, and want to convert volume units?
Tip: Our Density units converter will help you convert density units.
Do you want to convert mass units?
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
- statistics
- geometric average
- solid geometry
- pyramid
- frustum
- planimetrics
- polygon
- area of a shape
- goniometry and trigonometry
- cotangent
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Equilateral 83322
The glass weight has the shape of a regular four-sided pyramid with a base edge of 10 cm. The shell walls are equilateral triangles. What is the weight in grams of the paperweight if the density of the glass is 2500kg/m³? - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Quadrilateral 21523
Calculate the surface area and volume of a regular quadrilateral pyramid if the edge of the lower base is 18 cm and the edge of the upper base is 15 cm. The wall height is 9 cm. - Truncated pyramid
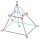The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
- Triangular 8227
The teacher cast the gold in the shape of a regular triangular pyramid with a base edge length of 12 cm and a height of 8 cm. The density of gold is 19,320 kg/m³. What is the weight of the casting? - Gravel - cone
The mound of gravel has a regular circular cone shape with a height of 3.3 meters and a base circumference of 18.85 meters. How many cubic meters of gravel are in a pile? Calculate the weight of gravel if its density is p = 640 kg/cubic m. - Calculate 81553
The picture puzzle made of wooden cubes weighs 0.792 kg. One cube has an edge length of 4 cm and a weight of 33 grams. Find out how many cubes make up a puzzle and calculate the wood density in kg/m³.
