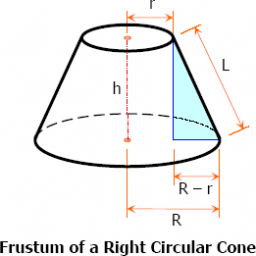
Cone - bases
The volume of the cut cone is V = 38000π cm3. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm.
Your answer:
Your answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Truncated cone 5
The height of a cone is 7 cm, the length of a side is 10 cm, and the lower radius is 3 cm. What could be the possible answer for the upper radius of a truncated cone? - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Two vases
Michaela has two vases in her collection. The first vase has the shape of a cone with a base diameter of d = 20 cm; the second vase has the shape of a truncated cone with a lower base of d1 = 25 cm and a diameter of the upper base d2 = 15 cm. Which vase c - Katy 7
Katy ordered a cylinder-shaped cake with a volume of 15.7 litres. It consists of two layers. The volume of the upper layer is 4 times smaller than the volume of the lower layer. The height of both layers is the same and equals the radius of the upper laye - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm. - Truncated pyramid
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base.
