Two vases

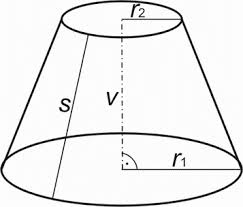
Michaela has two vases in her collection. The first vase has the shape of a cone with a base diameter d = 20 cm; the second vase has the shape of a truncated cone with the lower base d1 = 25 cm and with the diameter of the upper base d2 = 15 cm. Which vase can hold more water if the height of both vases is 0.5 m?

Correct answer:

V₁ =  5235.9878 cm³
V₂ =  5104.1667 cm³

Step-by-step explanation:

$$\begin{gathered} d=20\text{ cm } \\ {d}_1=25\text{ cm } \\ {d}_2=15\text{ cm } \\ h=0.5\text{ m}\to \text{ cm}=0.5\cdot 100\text{ cm}=50\text{ cm } \\ r=d\mathrm{/}2=20\mathrm{/}2=10\text{ cm } \\ {r}_1=d_1\mathrm{/}2=25\mathrm{/}2={\displaystyle \frac{25}{2}}=12.5\text{ cm } \\ {r}_2=d_2\mathrm{/}2=15\mathrm{/}2={\displaystyle \frac{15}{2}}=7.5\text{ cm } \\ {V}_1={\displaystyle \frac{1}{3}}\cdot \pi \cdot r^2\cdot h={\displaystyle \frac{1}{3}}\cdot 3.1416\cdot 10^2\cdot 50=5235.9878{\text{cm}}^3 \end{gathered}$$

$$\begin{gathered} S_1=\pi \cdot r_1^2=3.1416\cdot 12.5^2\doteq 490.8739{\text{cm}}^2 \\ {S}_2=\pi \cdot r_2^2=3.1416\cdot 7.5^2\doteq 176.7146{\text{cm}}^2 \\ {V}_2={\displaystyle \frac{1}{3}}\cdot h\cdot (S_1+\sqrt{S_1\cdot S_2}+S_2)={\displaystyle \frac{1}{3}}\cdot 50\cdot (490.8739+\sqrt{490.8739\cdot 176.7146}+176.7146)={\displaystyle \frac{30625}{6}}\doteq 5104.1667{\text{cm}}^3 \\ {V}_2<V_1 \\ \text{ Verifying Solution: } \\ {V}_2={\displaystyle \frac{1}{3}}\cdot h\cdot (r_1^2+r_1\cdot r_2+r_2^2)={\displaystyle \frac{1}{3}}\cdot 50\cdot (12.5^2+12.5\cdot 7.5+7.5^2){\text{cm}}^3={\displaystyle \frac{30625}{6}}{\text{cm}}^3=5104.1667{\text{cm}}^3 \end{gathered}$$

Try another example

Related math problems and questions:

• Frustum of a cone
  A reservoir contains 28.54 m³ of water when full. The diameter of the upper base is 3.5 m, while at the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone.
• Wooden bowls
  20 wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has a d
• Truncated cone 5
  The height of a cone 7 cm and the length of side is 10 cm and the lower radius is 3cm. What could the possible answer for the upper radius of truncated cone?
• Truncated pyramid
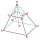  The truncated regular quadrilateral pyramid has a volume of 74 cm³, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's content. Calculate the area of the upper base.
• Runcated pyramid teapot
  The 35 cm high teapot has the shape of a truncated pyramid with the length of the edge of the lower square base a=50 cm and with the edges of the rectangular base b: 20 cm and c: 30 cm. How many liters of water will fit in the teapot?
• Truncated cone
  A truncated cone has bases with radiuses of 40 cm and 10 cm and a height of 25 cm. Calculate its surface area and volume.
• The cone
  The cone with a base radius of 12 cm and a height of 20 cm was truncated at a distance of 6 cm from the base, thus creating a truncated cone. Find the radius of the base of the truncated cone.
• Lamp cone
  Calculate the surface of a lampshade shaped of a rotary truncated cone with a base diameter of 32 cm and 12 cm and height of 24 cm.
• Octagonal prism vase
  0.7 l of water can be poured in an octagonal prism vase. What is the height of the vase, if the bottom has a area of 25 cm square and a thickness of 12 mm?
• Truncated cone
  Calculate the height of the rotating truncated cone with volume V = 794 cm³ and a base radii r₁ = 9.9 cm and r₂ = 9.8 cm.
• The truncated
  The truncated rotating cone has bases with radii r1 = 8 cm, r2 = 4 cm and height v = 5 cm. What is the volume of the cone from which the truncated cone originated?
• Rotary cone
  Rotary cone whose height is equal to the circumference of the base, has a volume 229 cm³. Calculate the radius of the base circle and height of the cone.
• Water overflow
  A rectangular container that has a length of 30 cm, a width of 20 cm, and a height of 24 cm is filled with water to a depth of 15 cm. When an additional 6.5 liters of water are poured into the container, some water overflows. How many liters of water over
• Truncated pyramid
  The concrete pedestal in the shape of a regular quadrilateral truncated pyramid has a height of 12 cm, the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base.
• Truncated cone 3
  The surface of the truncated rotating cone S = 7697 meters square, the substructure diameter is 56m and 42m, find the height of the tang.
• Cylinder horizontally
  The cylinder with a diameter of 3 m and a height/length of 15 m is laid horizontally. Water is poured into it, reaching a height of 60 cm below the axis of the cylinder. How many hectoliters of water is in the cylinder?
• Truncated cone
  Calculate the volume of a truncated cone with base radiuses r₁=13 cm, r₂ = 10 cm and height v = 8 cm.