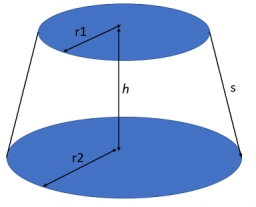
Frustum of a cone

A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone.

Correct answer:

h =  4.0005 m

Step-by-step explanation:

$$\begin{gathered} V=28.54{\text{m}}^3 \\ {D}_1=3.5\text{m} \\ {D}_2=2.5\text{m} \\ {r}_1=D_1/2=3.5/2=\frac{7}{4}=1.75\text{m} \\ {r}_2=D_2/2=2.5/2=\frac{5}{4}=1.25\text{m} \\ V=\frac{1}{3}\cdot \pi \cdot h(r_1^2+r_1\cdot r_2+r_2^2) \\ h=\frac{3\cdot V}{\pi \cdot (r_1^2+r_1\cdot r_2+r_2^2)}=\frac{3\cdot 28.54}{3.1416\cdot (1.75^2+1.75\cdot 1.25+1.25^2)}=4.0005\text{m} \end{gathered}$$

Try another example