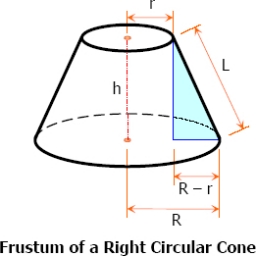
A concrete pedestal
A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume.
Your answer:
Your answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebraarithmeticsolid geometryplanimetryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Heptagonal pyramid
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Cone - bases
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - A lamp
A lamp shade like that of a frustum has a height of 12 cm and an upper and lower diameter of 10 cm and 20 cm. What area of materials is required to cover the curved surface of the frustum? - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Truncated pyramid
The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - Truncated pyramid
The concrete pedestal in a regular quadrilateral truncated pyramid has a height of 12 cm; the pedestal edges have lengths of 2.4 and 1.6 dm. Calculate the surface of the base. - Hourglass
An hourglass consists of two identical containers in the shape of rotational cones. For simplicity, we assume that the cones touch only at their apexes. The sand reaches to half the height of the lower cone. After turning the hourglass over, it takes exac
