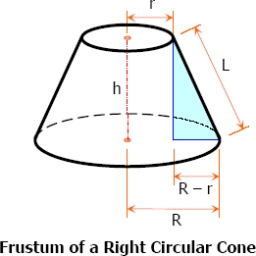
Zrezaný kužeľ
Betónový podstavec má tvar pravouhlého zrezaného kruhového kužeľa s výškou 2,5 metra. Priemer hornej a dolnej základne je 3 stopy a 5 stôp. Určte bočnú plochu povrchu, celkovú plochu povrchu a objem podstavca.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebraaritmetikastereometriaplanimetriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Zrezaný kúžeľ
Ak je nádrž úplne plná, nádrž obsahuje 28,54 m³ vody. Priemer hornej základne je 3,5 m, zatiaľ čo na spodnej základni je 2,5 m. Stanovte výšku, ak je nádrž v tvare zrezaného kužeľa pravouhlého kruhového kužeľa. - Zrezaný ihlan
Betónový podstavec tvaru pravidelného štvorbokého zrezaného ihlanu má výšku 12 cm, hrany podstavy majú dĺžky 2,4 a 1,6 dm. Vypočítaj povrch podstavca. - Objem 38
Objem zrezaného kužeľa je V=38000π cm³. Polomer dolnej podstavy je o 10 cm väčší, ako polomer hornej podstavy. Určte polomer podstáv, ak výška v=60 cm. - Betónový príklop
Betónový príklop na studňu kruhového tvaru má priemer 1300 mm a hrúbku 80 mm. Urč jeho hmotnosť v kg ak hustota betónu je 2545 kg/m3 - Kvetinová záhrada
Obdĺžniková kvetinová záhrada má rozmery 4 1/2 stopy x 4 3/4 stopy. Nájdite obvod a plochu záhrady. - Socha
Akú hmotnosť bude mať betónový podstavec tvaru kocky s dĺžkou hrany 10 m, ak jeden kubík betónu má hmotnosť 2200 kilogramov? - Valec
Nájdite objem a bočnú plochu valca s výškou 12 palcov a polomerom základne 4 palce.
