Komolý kruhový kužel
Betonový podstavec má tvar pravoúhlého komolého kruhového kužele s výškou 2,5 metru. Průměr horní a dolní základny je 3 stopy a 5 stop. Určete boční plochu povrchu, celkovou plochu povrchu a objem podstavce.
Vaše odpověď:
Vaše odpověď:
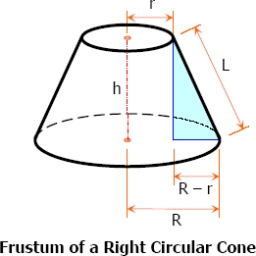
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieplanimetrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Komolý kužel
Pokud je nádrž zcela plná, nádrž obsahuje 28,54 m³ vody. Průměr horní základny je 3,5 m, zatímco na spodní základně je 2,5 m. Stanovte výšku, pokud je nádrž ve tvaru komolého kužele pravoúhlého kruhového kužele. - Komolý jehlan 4
Betonový podstavec tvaru pravidelného čtyřbokého komolého jehlanu má výšku 12 cm, hrany podstavy mají délky 2,4 a 1,6 dm. Vypočítej povrch podstavce. - Hmotnost betonového podstavce
Jakou hmotnost bude mít betonový podstavec tvaru kostky o délce hrany 10 m, pokud jeden kubík betonu má hmotnost 2200 kilogramů? - Kruhový kužel
Poloměr základny pravoúhlého kruhového kužele je 14 palců a jeho výška je 18 palců. Jaká je velikost boční strany? - Skleník 2
Skleník má tvar hranolu položeného na boční stěně. Podstavu tvoří lichoběžník a trojúhelník. Dolní základna lichoběžníku má délku 3 m, horní základna (a strana trojúhelníku) má délku 2 m, výška lichoběžníku je 1,8 m a výška trojúhelníku je 0,6 m. Výška hr - Příklop studna
Betonový příklop na studnu kruhového tvaru má průměr 1300 mm a tloušťku 80 mm. Urč jeho hmotnost v kg pokud hustota betonu je 2545 kg/m3 - Komolý kužel
Výška kužele je 7 cm a délka boční strany je 10 cm a spodní poloměr je 3 cm. Jaká by mohla být odpověď na horní poloměr komolého kužele?
