Příklady na kužel
Kužel je geometrické těleso, které vznikne rotací pravoúhlého trojúhelníku kolem jedné z jeho odvěsen.Hlavní části a vlastnosti kužele:
- Podstava – kruh, který tvoří spodní část kužele.
- Vrchol – nejvyšší bod kužele (mimo podstavy).
- Výška (v) – vzdálenost od vrcholu kužele k podstavě (kolmá vzdálenost).
- Strana kužele (plášť) – zakřivená plocha, která spojuje vrchol s podstavou.
- Průměr podstavy, (d=2r) – šířka podstavy.
- Poloměr podstavy (r) – polovina průměru podstavy.
Počet nalezených příkladů: 262
- Načrtni
Načrtni sít kužele a připiš k ní délku strany, délku oblouku kružnice a délku kružnice, když znáš: délku strany kužele: s = 51,9 cm obvod podstavy kužele= O =151 mm. - Kornout
Kolik kornoutů tvaru rotačního kužele budeme muset vzít pro naplnění 20l krémů (po okraj) má-li kornout vnitřní průměr podstavy 6 cm a výšku 8 cm. Udělej nákres, nápiš odpověď. - Zmrzlina 4
Sklenka na zmrzlinový pohár má tvar kužele. Její výška bez nožičky je 9cm a poloměr je 5 cm. Šimon si koupil osm kopečků zmrzliny, které mu na slunci všechny roztály. Jeden kopeček zmrzliny má objem 32 cm³. Kolik cm³ rozteklé zmrzliny vyteče přes okraj? - Objem kužele
Vypočítejte objem kužele s poloměrem podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Spočítej 3
Spočítej objem a hmotnost hromady písku tvaru kužele o průměru 8m a výšce v =4,5m, Hustota písku je 1500kg/M krychlový - Vypočítej kužel
Objem kužele je 461,58 cm3, jeho průměr je 14 cm. Vypočítej povrch tohoto kužele. - Kuželovitá
Kuželovitá nálevka má objem 0,5 litrů a výšku 7 cm. Vypočítejte poloměr jejího horního okraje. - Kužel těžký Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele.
- Kužel
Úsečka ležící na přímce y = -2x +9, která se nachází v kvadrantu I se otáčí okolo osy ya tím je tvořen kužel. Jaký je objem kužele? - Objem
Objem rotačního kužele je 376,8cm³, výška tohoto kužele je 1dm. Vypočtěte průměr podstavy kužele. - Poměr
Poloměry dvou kuželů jsou v poměru 5:7. Vypočítejte poměr objemů kuželů, které mají stejnou výšku. - Průměr 44
Průměr kužele je 24 cm, poloměr je 12 cm. Kolik cm měří výška, jestliže je o jednu třetinu větší než poloměr kužele? - Kužel
Rotační kužel s výškou h = 15 dm a poloměrem podstavy r = 2 dm rozřízneme rovinou rovnoběžnou s podstavou. Určitě vzdálenost vrcholu kužele od této roviny, jestliže vzniklé tělesa mají stejný objem. - Učitel
Učitel přinesl na hodinu dva dřevěné modely kuželů, které byly vyrobeny ze stejného druhu dřeva. První model vážil 800g. Druhý měl dvojnásobný poloměr podstavy, ale poloviční výšku. Urči hmotnost druhého kuželu v gramech. - Řezy kužele
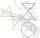Kužel s poloměrem podstavy 16 cm a výškou 16 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa. - Rotační kužel
Vypočítejte objem rotačního kužele o poloměru podstavy r=3 cm a výškou v=13 cm. - Zmrzlina
Ve zmrzlinovém kornoutu tvaru kužele o průměru 5,9 cm je 1,5 dl zmrzliny. Vypočtěte hloubku kornoutu. - Model 3
Model hradu má střechu ve tvaru kužele. Strana kužele je 45 cm dlouhá a poloměr podstavy je 27 cm. a) Jaký je objem střechy? b) Kolik dm² tapety se spotřebuje na polepení střechy, tedy pláště kužele? c) Jaká je hmotnost střechy, jestliže je vyrobena ze dř - Marie
Marie si chce ušít na maškarní ples čarodějnický klobouk ve tvaru kužele. Kolik materiálu bude potřebovat, když počítá s obrubou tvaru mezikruží s průměry 28cm a 44cm? Délka strany klobouku je 30cm. Připočítej 5% materiálu na zapošití. Zaokrouhli na cm². - Karnevalova čepice
Kolik dm² ozdobného papíru je potřeba ke zhotovení karnevalových čepic tvaru kužele pro 46 prvňáků, pokud obvod hlavy prvňáčka je 49 cm a výška čepice má být 33 cm. Na záhyby je nutné přidat 3% papíru?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám příklad a my Ti ho zkusíme vypočítat.
