Příklady na kužel - strana 13 z 14
Počet nalezených příkladů: 262
- Komolý kužel
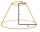Vypočtěte objem a povrch komolého kužele, pokud r1 = 12 cm, r2 = 5 cm a strana s = 10 cm. - Lampa
Vypočtěte povrch lampového stínítka tvaru rotačního komolého kužele s průměry podstav 32 cm a 12 cm a výškou 24 cm. - Komolý kužel
Vypočítejte povrch a objem komolého rotačního kužele s poloměry podstav 8 cm a 4 cm a výšce 5 cm. - Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r1=19 cm, r2 = 6 cm a výškou v = 22 cm. - Součástka - jehlanová
Ocelovou součástku ve tvaru seříznutého čtyřbokého jehlanu roztavili a vyrobili tři identické kostky. Určete povrch jedné kostky, pokud hrany postav jehlanu jsou 30 mm a 80 mm a výška jehlanu je 60 mm. Nevím si s tím nijak rády, nenašel jsem nikde řešení - Seříznutá součástka
Součástku tvaru seříznutého kužele s poloměry podstav 4 cm a 22 cm se má přetavit na součástku tvaru válce stejné výšky jako původní součástka. Jaký poloměr podstavy bude mít nová součástka? - Komolý jehlan
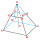Vypočítejte objem pravidelného 4-bokeho komolého jehlanu, jestliže a1 = 14 cm, a2 = 8 cm a úhel, který svírá boční stěna s podstavou je 42 stupňů. - Válec + čtyřstěn
Nádoba tvaru rotačního válce o poloměru podstavy 5 cm je naplněna vodou. O co stoupne hladina vody v nádobě, ponoříme-li do ní pravidelný čtyřstěn o hraně 7cm. - Komolý kužel
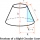Vypočtěte objem komolého kužele, jehož dna se skládají z vepsaného kruhu a kruhu odepsaného na protilehlých stěnách kostky s délkou hrany a = 1. - Koule v komolém kuželi
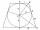Do komolého kužele o průměru podstav D1=10 cm a D2=20 cm, je vepsána koule, která se dotýká obou podstav i pláště. Jaký je její průměr? - Pod koulí
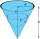Kolmý kruhový kužel s horní šířkou 24 cm a výškou 8 cm je naplněn vodou. V kuželu je ponořena kulová ocelová koule o poloměru 3,0 cm. Najděte objem vody pod koulí. - Stan pro 11 osob
Kuželový stan pojme 11 osob. Každý člověk potřebuje 4 m² prostoru na zemi a 20 m³ vzduchu k dýchání. Najděte výšku stanu. - Centimetre - rotace
Trojúhelník, jehož strany jsou 20 cm, 16 cm a 12 cm, se otáčí kolem své největší strany jako osy. Jaký je objem prostoru, který se generuje po úplné otáčce v kubických centimetrech? - Tavba dvou těles
Dvě pevné koule o poloměrech 2 cm a 4 cm se roztaví a přetaví do kužele o výšce 8 cm. Najděte poloměr takto vytvořeného kužele. - Vysvětlete 81386
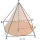Kužel má průměr x cm a výšku sklonu y cm. Čtvercový jehlan má délku strany základny x cm a výšku sklonu y cm. Který má větší povrch tělesa? Vysvětlete. - Těleso
Těleso má tvar kužele stojícího na polokouli, jehož oba poloměry se rovnají 1 cm a výška kužele se rovná jeho poloměru. Najděte objem tělesa. - Střed osy - kužel
Kužel o poloměru 10 cm je rozdělen na dvě části nakreslením roviny přes střed jeho osy, rovnoběžné s jeho základnou. Porovnejte objemy obou částí. - Stínítko lampy
Stínítko lampy má tvar seříznutého kužele s výškou sklonu 7 palců a poloměry základen 3 palce a 7 palců. Kolik materiálu se použije na jeho výrobu, je-li pro spoj povolen ¼ palce? - Seříznuty jehlan
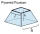Seříznutý jehlan se skládá ze čtvercové základny o délce 10 cm a vrchního čtverce o délce 7 cm. Výška seříznutého jehlanu je 6 cm. Vypočítejte povrch a objem. - Stínítko lampy
Stínítko lampy jako komolý má výšku 12 cm a horní a dolní průměr 10 cm a 20 cm. Jaká plocha materiálů je potřebná k pokrytí zakřiveného povrchu seříznutého okraje?
Máš příklad z matematiky, který jsi tady nenašel vyřešený? Pošli nám tenhle příklad a my Ti ho zkusíme vypočítat.
