Střed osy - kužel
Kužel o poloměru 10 cm je rozdělen na dvě části nakreslením roviny přes střed jeho osy, rovnoběžné s jeho základnou. Porovnejte objemy obou částí.
Vaše odpověď:
Vaše odpověď:
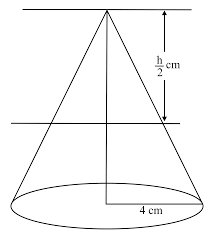
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikastereometriezákladní operace a pojmyJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Je dán 21
Je dán pravidelný čtyřboký jehlan s délkou podstavné hrany a=15 cm a výškou v=21 cm. Rovnoběžně s podstavou vedeme dvě roviny tak, že rozdělil výšku jehlanu na tři stejné části. Vypočítej poměr objemů vzniklých 3 těles. - V jedné třetině
Objem pravého kruhového kužele je 5 litrů. Vypočítejte objem dvou částí, na které je kužel rozdělen rovinou rovnoběžnou se základnou, v jedné třetině vzdálenosti od vrcholu k základně. - Odhad a přesná hodnota
A) odhadněte 0,34 x 0,063 zaokrouhlením obou čísel na jedno platné číslo b) vypočítejte přesnou hodnotu 0,34 x 0,063 porovnejte odpovědi na části a) a b) - Rozdělit řezem
Daný je kužel s poloměrem podstavy 10 cm a výšce 12 cm. V jaké výšce nad podstavou ho máme rozdělit řezem rovnoběžným s podstavou, aby objemy obou vzniklých teles byly stejné? Výsledek uveďte v cm. - Most přes řeku
Most přes řeku je ve tvaru oblouku kruhu s každou základnou mostu na břehu řeky. Ve středu řeky je most 10 stop (ft, feet) nad vodou. 27 stop od okraje řeky je most 9 metrů nad vodou. Jak široká je řeka? - Tečny ke kružnici
Ke kružnici o poloměru 76 mm jsou z bodu C vedeny dvě tečny. Vzdálenost obou dotykových bodů je 14 mm. Vypočítejte vzdálenost bodu C od středu kružnice. - Řezy kužele
Kužel s poloměrem podstavy 16 cm a výškou 16 cm rozdělíme rovinami rovnoběžnými s podstavou na tři tělesa. Roviny rozdělí výšku kužele na tři stejné části. Určete poměr objemů největšího a nejmenšího vzniklého tělesa.
