A cone 4
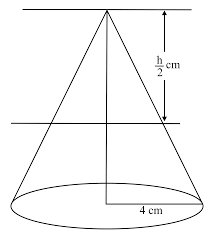
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
Your answer:
Your answer:
Tips for related online calculators
Check out our ratio calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticsolid geometrybasic operations and conceptsUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Right circular cone
The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - Cross-sections of a cone
Cone with base radius 15 cm and height 20 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Cutting cone
A cone with a base radius of 10 cm and a height of 12 cm is given. At what height above the base should we divide it by a section parallel to the base so that the volumes of the two resulting bodies are the same? Express the result in cm. - Pyramid volume ratio
A regular quadrilateral pyramid with base edge length a = 15 cm and height v = 21 cm is given. We draw two planes parallel to the base, dividing the height of the pyramid into three equal parts. Calculate the ratio of the volumes of the 3 bodies created. - 2x cone
A circular cone of height 36 cm is cut by a plane parallel to the base, dividing it into two smaller cones of equal volume. Calculate the height of the smaller cone. - Cone
A circular cone of height 14 cm and volume 4396 cm³ is cut at one third of its height (measured from the base) by a plane parallel to the base. Calculate the radius and circumference of the circular cross-section. - Cone
The circular cone has height h = 15 dm and base radius r = 2 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume.
