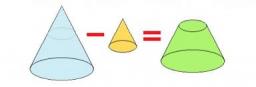
Cone
The circular cone of height 14 cm and volume 4396 cm3 is at one-third of the height (measured from the bottom) cut by a plane parallel to the base. Calculate the radius and circumference of the circular cut.
Correct answer:
Showing 3 comments:
Tips for related online calculators
Do you want to convert length units?
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebraarithmeticsolid geometryplanimetricsUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- 2x cone
Circular cone height 36 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Cone
The circular cone has height h = 29 dm and base radius r = 3 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume. - Right circular cone
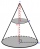The volume of a right circular cone is 5 liters. The cone is divided by a plane parallel to the base, one-third down from the vertex to the base. Calculate the volume of these two parts of the cone. - A cone 4
A cone with a radius of 10 cm is divided into two parts by drawing a plane through the midpoint of its axis parallel to its base. Compare the volumes of the two parts.
- Cross-sections of a cone
Cone with base radius 16 cm and height 11 cm divided by parallel planes to base into three bodies. The planes divide the height of the cone into three equal parts. Determine the volume ratio of the maximum and minimum of the resulting body. - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Pyramid cut
We cut the regular square pyramid with a parallel plane to the two parts (see figure). The volume of the smaller pyramid is 20% of the volume of the original one. The bottom of the base of the smaller pyramid has an area of 10 cm². Find the area of the or
