Similar frustums
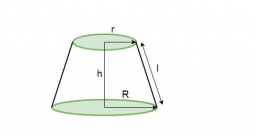
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums?
Your answer:
Your answer:
Showing 1 comment:
Math Student
m is radius of middle circle = radius of a bottom of upper frustum and radius of top of bottom frustum.
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Check out our ratio calculator.
Do you have a linear equation or system of equations and are looking for a solution? Or do you have a quadratic equation?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryalgebrasolid geometryplanimetrybasic operations and conceptsGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Heptagonal pyramid
A hardwood for a column is in the form of a frustum of a regular heptagonal pyramid. The lower base edge is 18 cm, and the upper base is 14 cm. The altitude is 30 cm. Determine the weight in kg if the wood density is 10 grams/cm³. - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - Cone - bases
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Wooden bowls
Twenty wooden bowls in the shape of a truncated cone should be painted on the outside and inside with wood varnish. We need 0.1 l of paint to paint 200 cm². How many liters of paint do we have to buy if the bowls are 25 cm high, the bottom of the bowl has - Truncated cone 5
The height of a cone is 7 cm, the length of a side is 10 cm, and the lower radius is 3 cm. What could be the possible answer for the upper radius of a truncated cone? - A concrete pedestal
A concrete pedestal has the shape of a right circular cone and a height of 2.5 feet. The diameters of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the pedestal's lateral surface area, total surface area, and volume. - Lamp shade
A lampshade is in the form of a frustum of a cone with a slant height of 7 inches and base radii of 3 inches and 7 inches respectively. How much material is used in its construction if 1/4 inch is allowed for the seam?
