Koule v komolém kuželi
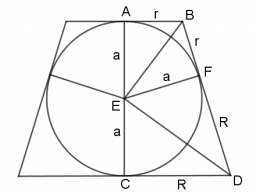
Do komolého kužele o průměru podstav D1=10 cm a D2=20 cm, je vepsána koule, která se dotýká obou podstav i pláště. Jaký je její průměr?
Vaše odpověď:
Vaše odpověď:
Zobrazuji 1 komentář:
Žák
Průměr vepsané koule se rovná součinu druhých odmocnin průměrů podstav komolého kužele.
6 let 1 Like
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraaritmetikastereometrieÚroveň náročnosti úkolu
Související a podobné příklady:
- Do rovnostranného 2
Do rovnostranného kužele s průměrem podstavy 12 cm je vepsána koule. Vypočtěte objem obou těles. Kolik procent objemu kužele vyplňuje vepsaná koule? - Rovnostranný válec
Do rovnostranného rotačního válce je vepsána koule (dotýká se podstav i pláště). Prokažte, že válec má objem i povrch o polovinu větší než koule do něj vepsaná. - Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r1=19 cm, r2 = 6 cm a výškou v = 22 cm. - Michaela
Michaela má ve své sbírce dvě vázy. První váza má tvar kužele s průměrem podstavy d = 20 cm; druhá váza má tvar komolého kužele s průměrem spodní podstavy d1 = 25 cm a s průměrem horní podstavy d2 = 15 cm. Do které vázy se vejde více vody, pokud výška obo - Vepsána kružnice krychle
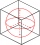Spodní podstavě krychle o hraně (a=1) je vepsána kružnice. Jaký poloměr má kulová plocha, která obsahuje tuto kružnici a jeden z rohů horní podstavy krychle? - Povrch koule
Vyjádři ve čtverečních centimetrech povrch koule, jejíž poloměr se rovná jedné čtvrtině poloměru kužele. Průměr podstavy kužele je 20 cm - Objem kulové vrstvy
Jaký je objem kulové vrstvy, která zůstane po odříznutí odstavců z obou stran koule, jejichž výška je 3,5 cm, Průměr koule je 24 cm.
