Vpísaná guľa

Do zrezaného komolého kužeľa s priemerom podstav D1=10 cm a D2=20 cm, je vpísaná guľa, ktorá sa dotýka oboch podstav i plášťa. Aký je jej priemer?

Správna odpoveď:

d =  14,1421 cm

Postup správneho riešenia:

D1​=10 cm D2​=20 cm  ABCD: a=D1​=10 cm c=D2​=20 cm b=d a+c = b+d = 2b  b=2a+c​=210+20​=15 cm  h=b2−(a/2−c/2)2​=152−(10/2−20/2)2​=10 2​ cm≐14,1421 cm  h=2r=d  d=h=14,1421=10 2​=14,1421 cm

Skúsiť iný príklad


Našiel si chybu či nepresnosť? Kľudne nám ju napíš.



Zobrazujem 1 komentár:
Dr. Math
Na vyriešenie tejto úlohy potrebujeme nájsť priemer gule vpísanej do komolého kužeľa s priemermi podstav D1 = 10 cm a D2 = 20 cm. Guľa sa dotýka oboch podstav aj plášťa kužeľa.

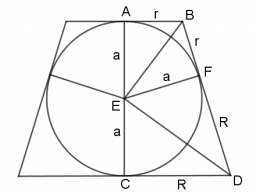
  Uvažujme rez komolým kužeľom a guľou rovinou prechádzajúcou osou. Rezom je lichobežník (komolý kužeľ) s vpísanou kružnicou (rez gule).

  Pre lichobežník s vpísanou kružnicou platí:
 
  a + c = b + d
 

  kde a = 2r1 = 10 cm, c = 2r2 = 20 cm, b = d = s (strany lichobežníka).

  Teda:
 
  10 + 20 = 2s ⇒ s = 15 cm
 

  Výška lichobežníka (komolého kužeľa) je:
 
  h = √s2 - (r2 - r1)2 = √152 - 52 = √225 - 25 = √200 = 10 √2 cm
 





Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:

algebraaritmetikastereometriaÚroveň náročnosti úlohy

 
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1

Súvisiace a podobné príklady: