Kužel těžký
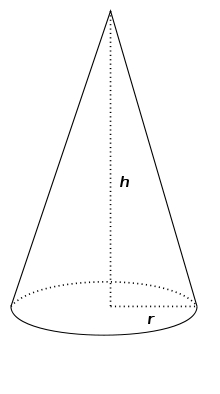
Povrch kužele je 200 cm², jeho výška je 7 centimetrů. Spočítej objem tohoto kužele.
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Hledáte pomoc s výpočtem kořenů kvadratické rovnice?
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
Máte lineární rovnici nebo soustavu rovnic a hledáte její řešení? Nebo máte kvadratickou rovnici?
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebrastereometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Objem rotačního kužele
Obsah pláště rotačního kužele je 240 cm² a obsah jeho podstavy 160 cm². Vypočítej objem tohoto kužele. - Vypočítej kužel
Objem kužele je 461,58 cm3, jeho průměr je 14 cm. Vypočítej povrch tohoto kužele. - Vypočítejte
Vypočítejte objem kužele, pokud obsah jeho podstavy je 78,5 cm² a obsah pláště je 219,8 cm². - Povrch a objem kužele
Výška je 5 cm a velikost úhlu, který svírá strana kužele s podstavou, je 63 stupňů. Vypočítej povrch a objem tohoto kužele. - Povrch válce z rozměrů
Určete povrch válce, pokud jeho průměr je 12 centimetrů a jeho výška se rovná 9 centimetrů. - Povrch a objem kužele
Vypočítej povrch a objem kužele, pokud průměr jeho podstavy je 12 cm a výška 150 mm. - Kužel - strana Vypočítejte povrch a objem kužele, jestliže jeho výška je 125 mm, a délka strany je 17 cm.
