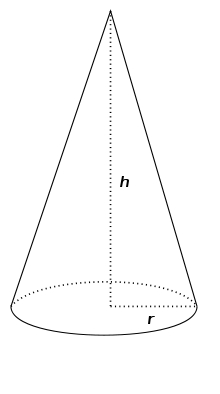
Hard cone problem
The cone's surface is 200 cm², and its height is 7 centimeters. Calculate the volume of this cone.
Correct answer:
Tips for related online calculators
Are you looking for help with calculating roots of a quadratic equation?
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
Do you have a linear equation or system of equations and looking for its solution? Or do you have a quadratic equation?
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
- algebra
- quadratic equation
- equation
- expression of a variable from the formula
- solid geometry
- cone
- surface area
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Surface of the cone
Calculate the cone's surface if its height is 8 cm and the volume is 301.44 cm³. - Calculate 30961
Calculate the cone's surface and volume if its base diameter is 12 cm and the height is 150 mm. - Calculate 28011
The volume of the cone is 9.42 cm3, and its base diameter is 3 cm. Calculate 1 / height of the cone 2 / side cones 3 / cone surface - Ratio
The radii of the two cones are in the ratio of 5.7. Calculate the area ratio of cones that have the same height. - Cone - side
Find the cone's surface area and volume if its height is 125 mm and the side length is 17 cm. - Volume of the cone
Calculate the cone's volume if its base area is 78.5 cm² and the shell area is 219.8 cm². - Cone area and side
Calculate a rotating cone's surface area and volume with a height of 1.25 dm and 17,8dm side. - Calculate 30971 Calculate the cone's surface and volume if its base diameter is 1 dm and the side length is 13 cm.
- Angle of deviation
The surface of the rotating cone is 30 cm² (with a circle base), and its surface area is 20 cm². Calculate the deviation of this cone's side from the base's plane. - Rotating cone Find the rotating cone's surface and volume if its side is 150 mm long and the circumference of the base is 43.96 cm.
- Calculate 30991 The volume of the cone is 461.58 cm³. Its diameter is 14 cm. Calculate the surface area of this cone.
- Slant height
The cone's slant height is 5cm, and the radius of its base is 3cm, so find the cone's volume. - Circumference 27581 The rotating cone has a base circumference of 62.8 cm. And a height of 0.7 dm. Calculate its surface area and volume.
- 2x cone
Circular cone height 84 cm was cut plane parallel with the base. The volume of these two small cones is the same. Calculate the height of the smaller cone. - Calculate 18843
Height 9cm diameter 24cm cone - calculate its volume and surface. - Calculate Calculate the cone's surface and volume from the rotation of the right triangle ABC with the squares 6 cm and 9 cm long around the shorter squeegee.
- Calculate 4689
The area of the rotating cone shell is 240 cm2, and the area of its base is 160 cm². Calculate the volume of this cone.
