Rotační kužel
Vypočítejte objem rotačního kužele o poloměru podstavy r=3 cm a výškou v=13 cm.
Správná odpověď:
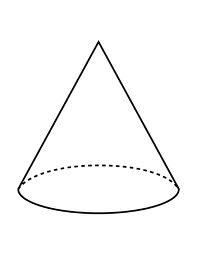
Zobrazuji 1 komentář:
Petra
Q: Nechápu proč pí má 3,1416 když pí má normálně 3,14 nevím zda to je správně, ale budu ráda kdybyste to tam aspoň vysvětlovali. Děkuji.
A: pí - Ludolfovo číslo je iracionálne a má nekonečný neperiodický desatinný rozvoj. Áno, bežne sa na ZDŠ používa 3,14 ... tj s presnosťou na dve desatinné miesta.
A: pí - Ludolfovo číslo je iracionálne a má nekonečný neperiodický desatinný rozvoj. Áno, bežne sa na ZDŠ používa 3,14 ... tj s presnosťou na dve desatinné miesta.
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Rot kužel
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=2,3 dm a výškou v=46 mm. - Rotační kužel II
Vypočítejte povrch rotačního kužele o poloměru podstavy r=17 cm a výškou v=16 cm. - Rotační kužel 5
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=4,6dm a výškou v=230mm. - Hromada štěrku
Hromada štěrku má tvar rotačního kužele s výškou 3,3 m a obvodem podstavy 18,85 m. Kolik metrů krychlových štěrku je v hromadě? Vypočítejte hmotnost štěrku, jestliže p = 640 kg/m krychlových.
- Objem kužele
Vypočítejte objem kužele s poloměrem podstavy r a výškou v. a) r = 6 cm, v = 8 cm b) r = 0,9 m, v = 2,3 m c) r = 1,4 dm, v = 30 dm - Základní 2
Základní parametry rotačního kužele jsou: Poloměr podstavy 5 cm Výška kužele 12 cm a strana kužele 13 cm. Vypočítej: a/objem kužele b/povrch kužele - Poměr obsahů
Poměr obsahu podstavy rotačního kužele k jeho plášti je 3:5. Vypočítejte povrch a objem kužele, pokud jeho výška v = 4 cm.
