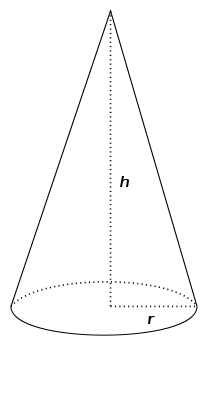
Objem kužele
Vypočítejte objem kužele s poloměrem podstavy r a výškou v.
a) r = 6 cm, v = 8 cm
b) r = 0,9 m, v = 2,3 m
c) r = 1,4 dm, v = 30 dm
Vaše odpověď:
a) r = 6 cm, v = 8 cm
b) r = 0,9 m, v = 2,3 m
c) r = 1,4 dm, v = 30 dm
Vaše odpověď:
Tipy na související online kalkulačky
Tip: Převody jednotky objemu vám pomůže naše kalkulačka pro převody jednotek objemu.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Válec horizontálně
Vypočítejte objem válce, je-li poloměr podstavy 3 cm a vztah mezi poloměrem podstavy a výškou válce je v = 3r - Rotační kužel 5
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=4,6 dm a výškou v=230 mm. - Rot kužel
Vypočítejte objem a povrch rotačního kužele o poloměru podstavy r=2,3 dm a výškou v=46 mm. - Kužel
Rotační kužel s výškou h = 15 dm a poloměrem podstavy r = 2 dm rozřízneme rovinou rovnoběžnou s podstavou. Určitě vzdálenost vrcholu kužele od této roviny, jestliže vzniklé tělesa mají stejný objem. - Seříznutý kužel
Vypočítejte objem komolého kužele s poloměry podstáv r1=19 cm, r2 = 6 cm a výškou v = 22 cm. - Hexa hranol
Vypočítejte objem a povrch pravidelného šestibokého hranolu s hranou podstavy a = 6 cm s příslušnou výškou v1 = 5,2 cm a výškou hranolu h = 1 dm. - PaO kužele
Rotační kužel má obvod podstavy 62,8 cm. A výšku 0,7 dm. Vypočítejte jeho povrch a objem.
