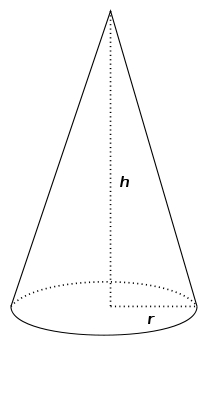
Volume of the cone
Find the volume of the cone with the base radius r and the height v.
a) r = 6 cm, v = 8 cm
b) r = 0,9 m, v = 2,3 m
c) r = 1,4 dm, v = 30 dm
Your answer:
a) r = 6 cm, v = 8 cm
b) r = 0,9 m, v = 2,3 m
c) r = 1,4 dm, v = 30 dm
Your answer:
Tips for related online calculators
Tip: Our volume units converter will help you convert volume units.
You need to know the following knowledge to solve this word math problem:
solid geometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Cone measurements
Calculate the volume and surface of the rotating cone with the base radius r = 4.6 dm and the height v = 230 mm. - Rotating cone
Calculate the volume of a rotating cone with base radius r=18 cm and height h=20 cm. - Rotating cone
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm. - Cone
The circular cone has height h = 15 dm and base radius r = 2 dm slice plane parallel to the base. Calculate the distance of the cone vertex from this plane if solids have the same volume. - Surface and volume
Calculate the surface and volume of a cylinder whose height is 8 dm and the radius of the base circle is 2 dm. - Cylinder surface area
The volume of a cylinder whose height is equal to the radius of the base is 678.5 dm³. Calculate its surface area. - Slant height
Find the cone's volume. The cone's slant height is 5 cm, and the radius of its base is 3 cm.
