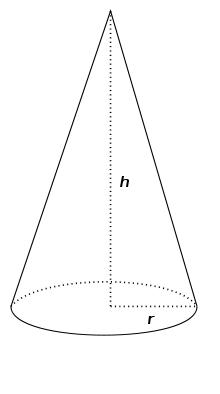
Rotating cone
Calculate the volume and the surface area of a rotating cone of base radius r = 2.3 dm and a height h = 46 mm.
Correct answer:
Tips for related online calculators
Do you want to convert length units?
Do you know the volume and unit volume, and want to convert volume units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Do you know the volume and unit volume, and want to convert volume units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Calculate 5789
Calculate the volume and surface of the rotating cone with the base radius r = 4.6dm and the height v = 230mm. - Rotating cone
How does the volume of the rotating cone change if: a) double the radius of the base b) We reduce the height three times c) Reduce the radius of the base five times - Rotating cone
Calculate the volume of a rotating cone with base radius r=8 cm and height h=18 cm. - Calculate 32281
The rotating cone has a base radius r = 226mm, and the deviation of the side from the base plane is 56 °. Calculate the height of the cone.
- Rotating cone II Calculate the area of the surface of a rotating cone with base radius r=15 cm and height h=13 cm.
- The rotating
The rotating cone has a height of 0.9 m, and the diameter of the base is 7.2 dm. Calculate the surface of the cone. (Hint: use Pythagorean theorem for a side of cone) - Parameters 28521
The basic parameters of the rotating cone are: Base radius 5 cm The cone height is 12 cm, and the cone side is 13 cm. Calculate: a/volume of the cone b/cone surface
