Truncated cone 5
The height of a cone is 7 cm, the length of a side is 10 cm, and the lower radius is 3cm. What could be the possible answer for the upper radius of a truncated cone?
Correct answer:
Tips for related online calculators
Do you want to convert length units?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
Units of physical quantities:
Grade of the word problem:
Related math problems and questions:
- Lampshade 7846
Lampshade for the face of a truncated cone with a height of 20 cm. The upper diameter of the shade is 13 cm, the lower 36 cm, and the side forms an angle of 60 degrees with the lower diameter. At least how much fabric is needed to make this shade? - Determine 73454
The volume of the cut cone is V = 38000π cm³. The radius of the lower base is 10 cm larger than the radius of the upper base. Determine the radius of the base if height v = 60 cm. - Two vases
Michaela has two vases in her collection. The first vase has the shape of a cone with a base diameter d = 20 cm; the second vase has the shape of a truncated cone with the lower base d1 = 25 cm and the diameter of the upper base d2 = 15 cm. Which vase can - Calculate 16513
The conical funnel has a volume of 0.5 liters and a height of 7 cm. Calculate the radius of its upper edge. - Frustrum - volume, area
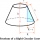Calculate the surface and volume of the truncated cone. The radius of the smaller figure is 4 cm, the height of the cone is 4 cm, and the side of the truncated cone is 5 cm. - Similar frustums
The upper and lower radii of a frustum of a right circular cone are 8 cm and 32 cm, respectively. If the altitude of the frustum is 10 cm, how far from the bottom base must a cutting plane be made to form two similar frustums? - Truncated pyramid
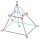The truncated regular quadrilateral pyramid has a volume of 74 cm3, a height v = 6 cm, and an area of the lower base 15 cm² greater than the upper base's area. Calculate the area of the upper base. - A concrete pedestal
A concrete pedestal has a shape of a right circular cone having a height of 2.5 feet. The diameter of the upper and lower bases are 3 feet and 5 feet, respectively. Determine the lateral surface area, total surface area, and the volume of the pedestal. - Double ladder
The double ladder shoulders should be 3 meters long. What height will the upper top of the ladder reach if the lower ends are 1.8 meters apart? - The cone
The cone has a base radius of 12 cm and a height of 20 cm. It was truncated at 6 cm from the base. We created a truncated cone - frustum. Find the radius of the base of the truncated cone. - Truncated cone
Calculate the volume of a truncated cone with base radiuses r1=13 cm, r2 = 10 cm, and height v = 8 cm. - Rotating cone
Calculate the volume of a rotating cone with base radius r=7 cm and height h=10 cm. - Probability 9771
What is the probability that ten molecules will arrange within the brown motion to be one molecule in the lower half and nine molecules in the upper half in one vessel? - Truncated cone
A truncated cone has bases with radiuses 40 cm and 10 cm and a height of 25 cm. Calculate its surface area and volume. - Frustum of a cone
A reservoir contains 28.54 m³ of water when complete. The diameter of the upper base is 3.5 m, while the lower base is 2.5 m. Find the height if the reservoir is in the form of a frustum of a right circular cone. - The surface
The surface of a truncated rotating cone with side s = 13 cm is S = 510π cm². Find the radii of the bases when their difference in lengths is 10cm. - Truncated cone
Find the volume and surface area of the truncated cone if r1 = 12 cm, r2 = 5 cm, and side s = 10 cm.
