Kotangens - příklady
V pravoúhlém trojúhelníku je kotangens definován jako poměr přilehlé odvěsny a protilehlé odvěsny. Je to převrácená hodnota tangens daného úhlu.Pokyny: Vyřešte každý úkol pečlivě a ukažte své celé řešení. Pokud je to vhodné, proveďte zkoušku správnosti řešení.
Počet nalezených příkladů: 37
- Úhel při 4
Úhel při vrcholu rovnoramenneho trojúhelníka má 78°. Základna 28,5cm. Délka ramen? - Horizontální 72204
Turista plánuje túru na jednu stranu hory a dolů na druhé straně vrcholu hory, přičemž každá strana hory je tvořena přímkou. Úhel elevace v počátečním bodě je 42,4 stupně a úhel elevace na konci je 48,3 stupně_ Horizontální vzdálenost mezi počátečním a ko - Tři geodeti
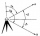Tři geodeti mají za úkol změřit výšku stožáru stojícího na rovné pláni. První měřič stojící 100 m od stožáru změřil výškový úhel (a), druhý vzdálený 200 m od stožáru změřil výškový úhel (b) a třetí ze vzdálenosti 300 m od stožáru změřil výškový uhel (c). - Příčný
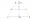Příčný řez kanálu má tvar lichoběžníku. Šířka dna je 2,25 m a hloubka 5 m. Stěny mají sklon 68° 12' a 73° 45'. Vypočítejte horní šířku kanálu.
- Tři sloupy
Vedle přímé cestě jsou tři sloupy vysoké 6 m ve stejné vzdálenosti 10 m. Pod jakým zorným úhlem vidí Vlado každý sloup, pokud je od prvního ve vzdálenosti 30 m a jeho oči jsou ve výšce 1,8 m? - Z okna
Z okna budovy ve výšce 7,5 m je vidět vrchol továrního komínu pod výškovým úhlem 76° 30′. Pata komínu je ze stejného místa vidět pod hloubkovým úhlem 5° 50′. Jak vysoký je komín? - Cesta
Na cestě je značka pro stoupání s úhlem 7%. Vypočtěte pod jakým úhlem (v stupních) cesta stoupá (klesá). - Stíhačka
Vojenská stíhačka letí ve výšce 10 km. Ze stanoviska na zemi byla zaměřena pod výškovým úhlem 23° a o 12 sekund později pod výškovým úhlem 27°. Vypočtěte rychlost stíhačky v km/hod. - TV tower
Vypočítejte výšku televizní věže, pokud pozorovatel, který stojí 430 m od paty věže vidí vrchol pod výškovým úhlem 23°?
- Žebřík
Žebřík se opírá o zeď ve výšce 7,5 m. Úhel sklonu žebříku je 76°. Jak daleko je spodní konec žebříku na zemi vzdálený od zdi? - Hloubkový úhel
Z pozorovací věže ve výšce 105 m nad hladinou moře je zaměřena loď v hloubkovém úhlu 1°49´. Jak daleko je loď od paty věže? - Pod hloubkovým úhlem
Záchranářský vrtulník je nad místem přistání ve výšce 180m. Místo záchranné akce je odsud vidět pod hloubkovým úhlem 52°40'. Jak daleko přistane vrtulník od místa záchranářské akce? - Východisko - mapa
Skauti měli postupovat lesem kolmo na jeho přímý okraj, kde byl cíl vzdálený od výchozího místa podle mapy 3 km. Od správného směru se odchýlili již ve východisku o 5°. Jak daleko od cíle vystoupili z lesa? - Sousedních 16793
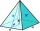Všechny boční hrany čtyřboké pyramidy ABCDV jsou stejně dlouhé a její základna je obdélník. Určete jeho objem, pokud znáte odchylky rovin sousedních bočních stěn a roviny základny a výšku h pyramidy.
- Dron
Létající dron zaměřoval území pro architekta. Vzlétl kolmo z bodu C do bodu D. Byl ve výšce 300 m nad rovinou ABC. Dron z bodu D zaměřil úhel BDC 43°. Vypočítejte v metrech vzdálenost bodů C a B. - Kužel
Vypočtěte objem a plochu kužele, jehož výška je 10 cm a v osovém řezu svírá se stěnou kužele úhel 30 stupňů. - Jehlan
Urči povrch pravidelného čtyřbokého jehlanu, když je dán jeho objem V = 120 a úhel boční stěny s rovinou podstavy je α = 42° 30'. - Tvrdé dřevo
Tvrdé dřevo pro sloup je ve tvaru komolého jehlanu, pravidelné heptagonálnej (hepta = 7) pyramidy. Dolní hrana základny je 18 cm a horní základna 14 cm. Výška je 30 cm. Zjistěte jeho hmotnost v kg, pokud je hustota dřeva 10 gramů / cm³. - Na vrcholu
Na vrcholu hory stojí hrad, který má věž vysokou 30m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou?
V trojúhelníku je dána délka strany AB = 6 cm, výška na stranu c = 5 cm, úhel BCA = 35°. Vypočítejte strany a, b.Máš úkol, nad kterým si lámeš alespoň 10 minut hlavu? Pošli nám úkol a my Ti ji zkusíme vypočítat. Řešení příkladů z matematiky.
