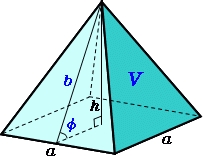
Pyramída
Všetky bočné hrany štvorbokej pyramídy ABCDV sú rovnako dlhé a jej základňa je obdĺžnik. Určte jeho objem, ak poznáte odchýlky rovín susedných bočných stien a roviny základne a výšku h pyramídy.
Vaša odpoveď:
Vaša odpoveď:
Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Tip: premeniť jednotky objemu vám pomôže naša kalkulačka premeny jednotiek objemu.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
algebrastereometriaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Odporúčame k tejto úlohe z matematiky si pozrieť toto výukové video: video1
Súvisiace a podobné príklady:
- Vypočítajte
Vypočítajte veľkosť odchýlky telesové uhlopriečky a bočné hrany c kvádra s rozmermi: a = 28 cm, b = 45 cm a c = 73 cm. Ďalej vypočítajte veľkosť odchýlky telesové uhlopriečkou od roviny podstavy. - Priesečník
Je daný pravidelný štvorboký ihlan ABCDV, vo vnútri jeho hrany AV je bod M, na preslúženej úsečke DC za bod C je bod N. Zostrojte priesečnicu roviny MNV s rovinou BCV a priesečník priamky MN a roviny BCV. - Štvorboký ihlan
Vypočítajte objem a povrch pravidelného 4bokého ihlanu, ktorého podstavná hrana je dlhá 4 cm. Odchýlka bočných stien od roviny je 60 stupňov. - Roviny bočných sien
Vypočítaj objem a povrch kvádra ktorého strana c má dĺžku 30 cm a telesová uhlopriečka zviera s rovinami bočných stien uhlami o veľkostiach 24 st. 20′, 45 st. 30′ - Kov modelu
Peter si z dovolenky v Egypte priviezol model pyramídy v tvare pravidelného štvorbokého ihlanu. Zmeral si že jej podstavná hrana má dĺžku 7 cm a bočné hrany majú dĺžku 10 cm. Model má hmotnosť 1 kg a je vyrobený z neznámeho kovu. Z akého kovu je model vyr - 4B ihlan - 3 časti
Je daný pravidelný štvorboký ihlan s dĺžkou podstavnej hrany a = 15 cm a výškou v = 21 cm. Rovnobežne s podstavou vedieme dve roviny tak, že rozdelil výšku ihlanu na tri rovnaké časti. Vypočítaj pomer objemov vzniknutých troch telies. - Kváder
Kváder má objem 768 cm³ a hrany označené x sú rovnako dlhé. Vypočítajte hodnotu x.
