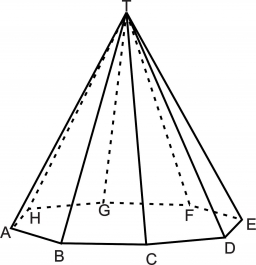
Octagonal pyramid
Find the volume of a regular octagonal pyramid with height v = 100 and the angle of the side edge with the base plane is α = 60°.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
Tip: Our volume units converter will help you convert volume units.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
algebrasolid geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- In a regular 5
In a regular triangular prism ABCV, the deviation of the side wall and the base plane is α = 45°. Determine the deviation of the side edge and the base plane. - Quadrilateral pyramid
The regular quadrilateral pyramid has a base edge a = 1.56 dm and a height h = 2.05 dm. Calculate: a) the deviation angle of the sidewall plane from the base plane b) deviation angle of the side edge from the plane of the base - Tetrahedral pyramid 8
Let all the side edges of the tetrahedral pyramid ABCDV be equally long and its base let us be a rectangle. Find its volume if you know the deviations A=52° B=56° between the planes of adjacent sidewalls and the base plane. The height of the pyramid is h= - 4side pyramid
Calculate the volume and surface of the regular four-sided pyramid whose base edge is 4 cm long. The angle from the plane of the sidewall and base plane is 60 degrees. - Regular quadrangular pyramid
How many square meters are needed to cover the shape of a regular quadrangular pyramid base edge of 10 meters if the deviation lateral edges from the base plane are 68°? Calculate waste 10%. - Quadrangular pyramid
Calculate the surface area and volume of a regular quadrangular pyramid: sides of bases (bottom, top): a1 = 18 cm, a2 = 6cm angle α = 60 ° (Angle α is the angle between the sidewall and the base plane.) S =? , V =? - Tetrahedral pyramid
Determine the surface of a regular tetrahedral pyramid when its volume is V = 120 and the angle of the sidewall with the base plane is α = 42° 30'.
