Kvádr
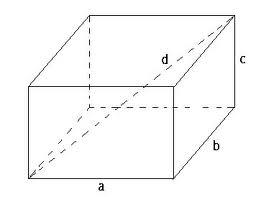
Určete rozměry kvádru a, b, c pokud tělesova úhlopříčka d=10 dm svírá s hranou a úhel α=52° a s hranou b úhel β=63°
Správná odpověď:
Tipy na související online kalkulačky
Chcete proměnit jednotku délky?
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
stereometrieplanimetriečíslagoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Úhlopříčka
Určete rozměry kvádru, pokud tělesova úhlopříčka dlouhá 49 dm svíra s jednou hranou úhel 61° a s druhou hranou úhel 66°. - Čtverečních 6951
Vypočítej chybějící rozměr v obdélníku, pokud znáš: S= 51,66 dm čtverečních, a=8,2 dm - Čtyřboký hranol
Výška pravidelného čtyřbokého hranolu je v = 10 cm, odchylka tělesových úhlopříčky od podstavy je 60°. Určete délku podstavových hran, povrch a objem kvádru. - Telesová
Kvádr má rozměry d = 5 cm, š = 4 cm a v = 3 cm. Vypočítej délku jeho telesové úhlopríčky. - Kvádr
Vypočítejte úhel který svírá podstava kvádru 11 × 10 s tělesových úhlopříčkou dlouhou 19. - Vypočítejte 3950
Vypočítejte tělesovou úhlopříčku kvádru, jehož rozměry jsou: a=3cm, b=5, c=7cm. Určete i jeho objem. - Vypočítejte 248
Vypočítejte objem a povrch pravidelného čtyřbokého hranolu o podstavné hraně a=24 cm, jestliže tělesová úhlopříčka svírá s podstavou úhel 66°
