Vektory v prostoru
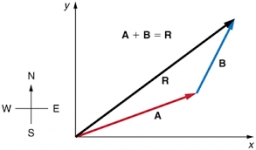
Dáno jsou vektory u = (1; 3; -4), v = (0; 1; 1). Určete velikost těchto vektorů, Vypočtěte úhel vektorů, vzdálenost mezi vektory.
Správná odpověď:
Zobrazuji 2 komentáře:
Petra
Absolutně nechápu, co je myšleno tímto výpočtem c = (ux.vx + uy + vy + uy.vy)/a.b. Podle mě je to absolutní nesmysl. Odchylka dvou vektorů se počítá takto: cosA=u.v/|u|.|v|
V čitateli je skalární součin u.v pro který platí u.v=ux.vx+uy.vy+uz.vz.
také moc nechápu výpočet vzdálenosti mezi vektory. w=u-v je rozdíl dvou vektorů, ale podle mě to není vzdálenost vektorů. Nedává my smysl určovat vzdálenost u vektorů, které nejsou rovnoběžné (v rovině), případně mimoběžné (v prostoru). Dva vektory z vašeho příkladu jsou různoběžné a počítat jejich vzdálenost nemá smysl.
V čitateli je skalární součin u.v pro který platí u.v=ux.vx+uy.vy+uz.vz.
také moc nechápu výpočet vzdálenosti mezi vektory. w=u-v je rozdíl dvou vektorů, ale podle mě to není vzdálenost vektorů. Nedává my smysl určovat vzdálenost u vektorů, které nejsou rovnoběžné (v rovině), případně mimoběžné (v prostoru). Dva vektory z vašeho příkladu jsou různoběžné a počítat jejich vzdálenost nemá smysl.
Tipy na související online kalkulačky
Potřebujete pomoci sčítat, zkrátít či vynásobit zlomky? Zkuste naši zlomkovou kalkulačku.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Kosinovú větu přímo používá kalkulačka SUS trojúhelníku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
Související a podobné příklady:
- Vektory
Pro vektor w platí: w = +4v. UrčPro vektor w platí: w = +4v. Určete souřadnice vektoru w, jestliže u=(-4, 2), v=(0, 3) - Vektory - základní operace
Dáno jsou body A [-11; 14] B [-1; -18] C[10; -20] a D[19; 15] a. Určitě souřadnice vektorů u = AB v = CD s = DB b. Vypočítejte vektorový součet u + v c. Vypočítejte rozdíl vektorů u-v d. Určitě souřadnice vektoru w = -4.u - Jsou dány 2
Jsou dány vektory v=(2,7; -1,8), w=(-3;2,5). Určete souřadnice vektorů: a=v+w, b=v-w, c=w-v, d=2/3v - Vektory
Urči velikost vektorů u= (2,4) a v= (-3,3)
- Určete 20
Určete velikost úhlu mezi vektory u =(3; -5) a v = (10;6) - Určete 19
Určete neznámou souřadnici vektoru tak, aby vektory byly kolineární: e=(7, -2), f = (-2, f2) c= ( -3/7, c2), d=(-4,0) - Vektorový součet
Velikost vektoru u je 4, vektoru v je 10. Vektory svírají úhel 60 °. Jaká je velikost vektoru u + v? - Vektor
Vypočtěte velikost vektoru v&; 8407; = (-1,5, 4,5, 3, 4,5, -6,75, -4,75) - Vektory Vektor a má souřadnice (-7; 18) a vektor b má souřadnice (11; 19). Pokud vektor c = b - a, jaká je velikost vektoru c?
- Kolmá a rovnoběžná
Potřebuji matematickou pomoc v tomto problému: jsou dány dva trojrozměrné vektory a = (- 5, 5 3) b = (- 2, -4, -5) Rozložte vektor b na b = v + w, kde v je rovnoběžná s a a w je kolmá na a. Najděte souřadnice vektorů v a w. - Je dán 15 Je dán koncový bod vektoru, který je umístěn v počátku kartézské soustavy Oxy. Určete souřadnice vektoru, jeho velikost a načrtněte jej: P[3,4] ; Q[-2,7] ; S[-5,-2] . .. tj. Vektory PO, QO, SO
- Tři síly - vektory
Tři síly, jejichž velikosti jsou v poměru 9:10:17, působí v rovině v jednom bodě tak, že jsou v rovnováze. Určete velikosti úhlů, které svírají každé dvě síly - Parametrické 2595
Vypočítat vnitřní úhly trojúhelníku ABC pomocí vektorů. Souřadnice A[2;4] B[4;6] C[0;-4]. Vypočítat směrové vektory stran, parametrické a obecně rovnice stran, parametrické a obecné rovnice těžnic, vypočítat obsah, vypočítat výšku. - Trojúhelník
Je dán trojúhelník KLM souřadnicemi vrcholů v rovině: K[-3, 15] L[3, -1] M[-19, 1]. Vypočítejte jeho obsah a vnitřní úhly.
- Vektory 82034
Dány jsou vektory a = (3, -2), b = (-1, 5). Určete vektor c, pro který platí a. c = 17; c = 3 - Najděte
Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Pravoúhlý 19
Pravoúhlý trojúhelník. Je dáno: strana c=15,8 a úhel alfa=73°10' Výpočtete stranu a, b, úhel beta a obsah
