Angle between vectors
Find the angle between the given vectors to the nearest tenth degree. u = (6, 22) and v = (10, -11)
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
The Pythagorean theorem is the base for the right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
The Pythagorean theorem is the base for the right triangle calculator.
Most natural application of trigonometry and trigonometric functions is a calculation of the triangles. Common and less common calculations of different types of triangles offers our triangle calculator. Word trigonometry comes from Greek and literally means triangle calculation.
You need to know the following knowledge to solve this word math problem:
geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Space vectors 3D
The vectors u = (1; 3;- 4) and v = (0; 1; 1) are given. Find their sizes, calculate their angles, and determine the distances between them. - A ship
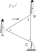A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° - Scalar dot product
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - Measurements of a triangle
Find the area of the triangle with the given measurements. Round the solution to the nearest hundredth if necessary. A = 50°, b = 30 ft, c = 14 ft
- Vectors
Find the magnitude of the angle between two vectors u = (3; -5) and v = (10; 6) - Black diamond run
Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet. - An isosceles triangle
An altitude is drawn from the vertex of an isosceles triangle, forming a right angle and two congruent triangles. As a result, the altitude cuts the base into two equal segments. The length of the altitude is 18 inches, and the length of the base is 15 in
