Úhel mezi vektory
Najděte úhel mezi danými vektory a zaokrouhlete výsledek na desetinu stupně.
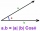
u = (1, 9) a v = (-14, 14)
Vaše odpověď:
u = (1, 9) a v = (-14, 14)
Vaše odpověď:
Zobrazuji 2 komentáře:
Tipy na související online kalkulačky
Dva vektory určeny velikostmi a vzájemným úhlem sčítá naše kalkulačka sčítání vektorů .
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Víte objem a jednotku objemu a chcete proměnit jednotku objemu?
Pythagorova věta je základ výpočtů kalkulačky pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriearitmetikaplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- Obsah trojúhelníku s danými rozměry
Najděte obsah trojúhelníku s danými rozměry. V případě potřeby zaokrouhlete řešení na nejbližší setinu. A = 50°, b = 30 stop, c = 14 stop - Najděte
Najděte vektor v4 kolmý na vektory v1 = (1, 1, 1, -1), v2 = (1, 1, -1, 1) a v3 = (0, 0, 1, 1) - Bazén 5
Obdélníkový nafukovací bazén má 3 yardy na délku, 2 5/8 yardu na šířku a 1 3/5 yardu na výšku. Jaký je objem bazénu? Zaokrouhlete výsledek na nejbližší desetinu. - Rovnoramenný trojuholník
Výška je nakreslena z vrcholu rovnoramenného trojúhelníku, který tvoří pravý úhel a dva shodné trojúhelníky. Výsledkem je, že výška rozděluje základnu na dva stejné segmenty. Délka výšky je 18 palců a délka základny je 15 palců. Najděte obvod trojúhelníku - Krabice/kvádr
Jaký je objem krabice s těmito rozměry: V = 1,5 dm Š = 3,5 dm D = 45 cm Odpověď uveďte v dm³ a zaokrouhlete na nejbližší desetinu. - Trojúhelník - kosinova věta
Vyřešte chybějící rozměry pro následující trojúhelník: Trojúhelník ABC: Úhel A=43 stupňů, b=7,0 cm, c=6,0 cm Otázka 1. Úhel B s jednotkami zapsanými jako stupně Otázka 2. Úhel C s jednotkami zapsanými jako stupně Otázka 3.a, zaokrouhlená na nejbližší dese - Geodet
Geodet odhadl vzdálenost přes řeku na 300m. Skutečná vzdálenost přes řeku byla 286,4m. Najděte absolutní chybu a procentuální chybu odhadu geodeta. Pokud je to nutné, zaokrouhlete na nejbližší desetinu.
