Black diamond run
Taleah is skiing down a black diamond run. She begins skiing at the top of a ski trail whose elevation is about 8625 feet. The ski run ends toward the base of the mountain at 3800 feet. The horizontal distance between these two points is about 4775 feet. Find the elevation angle to the top of the ski run to the nearest tenth.
Final Answer:

Tips for related online calculators
Do you want to round the number?
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
arithmeticplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- A hiker
 A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - A radio antenna
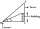 Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from - Kenyon
 Kenyon was hiking on a mountain. He stopped to rest at an elevation of 75 feet. He then continued on to the top. The elevation at the tip was 200 feet. How far did he climb after his break?
Kenyon was hiking on a mountain. He stopped to rest at an elevation of 75 feet. He then continued on to the top. The elevation at the tip was 200 feet. How far did he climb after his break? - Skiing
 The ski gondola starts at a distance of 975 m from the top and is 389 meters long. I went from the bottom station to the top station. How many meters must I go to the top of the hill?
The ski gondola starts at a distance of 975 m from the top and is 389 meters long. I went from the bottom station to the top station. How many meters must I go to the top of the hill? - Mountain railway
 The railway line's height difference between points A and B is 38.5 meters. Their horizontal distance is 3.5 km. Determine the average climb in permille up the track.
The railway line's height difference between points A and B is 38.5 meters. Their horizontal distance is 3.5 km. Determine the average climb in permille up the track. - Consider 6
 Consider the following word problem: The temperature readings for 20 days at 1 AM at a local ski resort were recorded as follows: 9° 27° −4° 1° 5° 14° 6° 28° −2° 16° 30° 4° 20° 30° −5° 15° −7° 25° −1° 5° What was the average of the recorded temperatures f
Consider the following word problem: The temperature readings for 20 days at 1 AM at a local ski resort were recorded as follows: 9° 27° −4° 1° 5° 14° 6° 28° −2° 16° 30° 4° 20° 30° −5° 15° −7° 25° −1° 5° What was the average of the recorded temperatures f - The tower
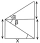 From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
From a window 8 m above the horizontal plane, we can see the top of the tower at an elevation angle of 53 degrees 20 minutes, and its base at an angle of 14 degrees 15 minutes. How high is the tower?
