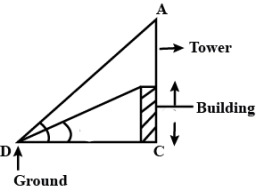
A radio antenna
Avanti is trying to find the height of a radio antenna on the roof of a local building. She stands at a horizontal distance of 21 meters from the building. The angle of elevation from her eyes to the roof (point A) is 42°, and the angle of elevation from her eyes to the top of the antenna (point B) is 51°. If her eyes are 1.54 meters from the ground, find the height of the antenna (the distance from point A to point B). Round your answer to the nearest meter if necessary.
Final Answer:
Tips for related online calculators
See also our right triangle calculator.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
planimetrygoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Angle of elevation
From a point A on the ground, the angle of elevation of the top of a 20 m tall building is 45°. A flag is hoisted at the top of the building, and the angle of elevation of the top of the flagpole from A is 60°. Find the length of the flagpole and the dist - Angles of elevation
From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37°, respectively. If |AB| = 57 m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side o - Tower + pole
On horizontal ground, there is a vertical tower with a flagpole on its top. From a point 9 m from the foot of the tower, the angles of elevation of the top and bottom of the flagpole are 60° and 30° respectively. Find the height of the flagpole. - The angle 9
The angle of elevation of the top of a tower from a point A on the ground is 30°. On moving 20 m closer to the foot of the tower to a point B, the angle of elevation increases to 60°. Find the height of the tower and the distance of the tower from point A - Two men 2
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 45°, respectively. If the height of the tower is 50 m, find the distance between the two men. - Elevation of the tower
We can see the top of the tower standing on a plane from a certain point A at an elevation angle of 39°25''. If we come towards its foot 50 m closer to place B, we can see the top of the tower from it at an elevation angle of 56°42''. How tall is the towe - Angle of elevation
The angle of elevation of the top of an unfinished pillar at a point 150 m from its base is 30°. If the angle of elevation at the same point is to be 45°, then the pillar has to be raised to a height of how many meters?
