Observation tower

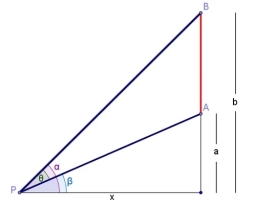
At the top of the hill, there is a 30-meter-high observation tower. We can see its heel and shelter from a certain point in the valley at elevation angles a=28°30" and b=30°40". How high is the top of the hill above the horizontal plane of the observation point?

Final Answer:

y =  325.6807 m

Step-by-step explanation:

$$\begin{gathered} v=30\text{m} \\ \alpha =28°30^{\prime }=28°+\frac{30}{60}°=28.5°=28.5 \\ \beta =30°40^{\prime }=30°+\frac{40}{60}°=30.6667°\doteq 30.6667 \\ {t}_2=\tan (\beta )=\tan (30.6667°)\doteq 0.593 \\ {t}_1=\tan (\alpha )=\tan (28.5°)\doteq 0.543 \\ \tan \alpha =\frac{x}{v+y} \\ \tan \beta =x:y \\ x=y\cdot \tan \beta \\ y\cdot \tan \beta /\tan \alpha =v+y \\ y(\tan \beta /\tan \alpha -1)=v \\ y=\frac{v}{t_2/t_1-1}=\frac{30}{0.593/0.543-1}\doteq 325.6807\text{m} \\ \text{ Verifying Solution: } \\ x=y\cdot t_2=325.6807\cdot 0.593\doteq 193.1188\text{m} \end{gathered}$$

Try another example