Výška kopce s rozhlednou
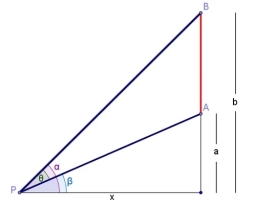
Na vrcholu kopce stojí rozhledna 30 m vysoká. Její patu a vrchol vidíme z určitého místa v údolí pod výškovými úhly a=28°30", b=30°40". Jak vysoko je vrchol kopce nad horizontální rovinou pozorovacího místa?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
planimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Z okna 2
Z okna ležícího 8 m nad horizontální rovinou vidíme vrchol věže ve výškovém úhlu 53 stupňů 20 minut, její patu v hloubkovém úhlu 14 stupňů 15 minut. Jak vysoká je věž? - Na vrcholu
Na vrcholu hory stojí hrad, který má věž vysokou 30 m. Křižovatku cest v údolí vidíme z vrcholu věže a od její paty v hloubkových úhlech 32° 50 'a 30° 10'. Jak vysoko je vrchol hory nad křižovatkou? - Pozorovatel
Pozorovatel vidí patu věže vysoké 96 metrů pod hloubkovým úhlem 30 stupňů a 10 minut a vrchol věže pod hloubkovým úhlem 20 stupňů a 50 minut. Jak vysoko je pozorovatel nad vodorovnou rovinou, na níž stojí věž? - Triangulace - výškové úhly
Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50 m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž? - Výška stožáru z úhlů
Vypočítejte výšku stožáru, jehož patu vidíme v hloubkovém úhlu 11° a vrchol ve výškovém úhlu 28°. Stožár je pozorován z místa 10 m nad úrovní paty stožáru. - Rozhledna a turista
Jak daleko od rozhledny vysoké 48 m stal turista, pokud její vrchol viděl pod úhlem o velikosti 40°? - Usu
Ze dvou míst A B na vodorovné rovině bylo pozorováno čelo mraku nad spojnicí obou míst pod výškovým úhlem 73°20' a 64°40'. Místa A B jsou od sebe vzdálená 2830 m. Jak vysoko je mrak?
