Pozorovatel
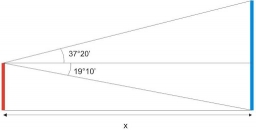
Pozorovatel vidí patu věže vysoké 96 metrů pod hloubkovým úhlem 30 stupňů a 10 minut a vrchol věže pod hloubkovým úhlem 20 stupňů a 50 minut. Jak vysoko je pozorovatel nad vodorovnou rovinou, na níž stojí věž?
Vaše odpověď:
Vaše odpověď:
Tipy na související online kalkulačky
Vyzkoušejte naši kalkulačka na přepočet poměru.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Máte soustavu rovnic a hledáte kalkulačku soustavy lineárních rovnic?
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
algebraplanimetriezákladní operace a pojmygoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Související a podobné příklady:
- Z okna 2
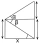Z okna ležícího 8 m nad horizontální rovinou vidíme vrchol věže ve výškovém úhlu 53 stupňů 20 minut, její patu v hloubkovém úhlu 14 stupňů 15 minut. Jak vysoká je věž? - TV tower
Vypočítejte výšku televizní věže, pokud pozorovatel, který stojí 430 m od paty věže vidí vrchol pod výškovým úhlem 23°? - Výška kopce s rozhlednou
Na vrcholu kopce stojí rozhledna 30 m vysoká. Její patu a vrchol vidíme z určitého místa v údolí pod výškovými úhly a=28°30", b=30°40". Jak vysoko je vrchol kopce nad horizontální rovinou pozorovacího místa? - Zrcátko
Jak daleko od svých nohou musel Pavel umístit zrcátko, aby v něm uviděl vrchol věže vysoké 12 m? Výška Pavlových očí očí nad vodorovnou rovinou je 160 cm, Pavel je od věže vzdálen 20 m. - Z rozhledně
Z rozhledně vysoké 40 m je vidět vrchol topolu pod hloubkovym uhlem o velikosti 50°10' a patu topolu v hloubkovem úhlu o velikosti 58°. Vypocitejte výšku topolu. - Západ-jih
Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž? - Hloubkový úhel
Maják vidí loď pod hloubkovým úhlem 25°. Pozorovatel z majáku je ve výšce 82 m nad mořem. Jak daleko je loď od vrchu majáku?
