Západ-jih
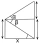
Pozoroval stojící západně od věže vidí její vrchol pod výškovým úhlem 45 stupňů. Poté, co se posune o 50 metrů na jih, vidí její vrchol pod výškovým úhlem 30 stupňů. Jak vysoká je věž?
Vaše odpověď:
Vaše odpověď:
Zobrazuji 2 komentáře:
Žák
Asi by stálo za úvahu, opravit výšku věže o výšku očí pozorovatele (nebo výšku měřícího přístroje).
Zs Ucitel
nj, v zadani se o vyske oci nic nepise... tj. vyska oci = zakladna od ktere pocitame ...
Tipy na související online kalkulačky
Vyzkoušejte také naši kalkulačku pravouhlého trojuholníka.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
Vyzkoušejte také naši trigonometrickou trojúhelníkovou kalkulačku.
Vyzkoušejte si převody jednotek úhlů úhlové stupně, minuty, sekundy, radiány.
K vyřešení této úlohy jsou potřebné tyto znalosti z matematiky:
geometriealgebraaritmetikaplanimetriegoniometrie a trigonometrieJednotky fyzikálních veličinÚroveň náročnosti úkolu
Doporučujeme k tomuto príkladu si prohlédnout toto výukové video: video1
Související a podobné příklady:
- TV tower
Vypočítejte výšku televizní věže, pokud pozorovatel, který stojí 430 m od paty věže vidí vrchol pod výškovým úhlem 23°? - Pozorovatel
Pozorovatel vidí patu věže vysoké 96 metrů pod hloubkovým úhlem 30 stupňů a 10 minut a vrchol věže pod hloubkovým úhlem 20 stupňů a 50 minut. Jak vysoko je pozorovatel nad vodorovnou rovinou, na níž stojí věž? - Vrchol Eiffelově věži
Vrchol Eiffelově věži vidíme ze vzdálenosti 600 metrů pod úhlem 30 stupňů. Určete výšku věže. - Pozorovatel 11
Pozorovatel vidí letadlo pod výškovým úhlem 35° (úhel od vodorovné roviny). V tu chvíli letadlo hlásí výšku 4 km. Jak daleko od pozorovatele je místo, nad kterým letadlo letí. Zaokrouhli na stovky metrů. - Triangulace - výškové úhly
Vrchol věže stojící na rovině vidíme z určitého místa A ve výškovém úhlu 39° 25´. Přijdeme-li směrem k jeho patě o 50 m blíže na místo B, vidíme z něho vrchol věže ve výškovém úhlu 56° 42´. Jak vysoká je věž? - Z okna 2
Z okna ležícího 8 m nad horizontální rovinou vidíme vrchol věže ve výškovém úhlu 53 stupňů 20 minut, její patu v hloubkovém úhlu 14 stupňů 15 minut. Jak vysoká je věž? - Z věže
Z věže 15 metrů vysoké a od řeky 30 metrů vzdálené se jevila šířka řeky v úhlu 15°. Jak široká je řeka v tomto místě?
