Výškový uhol
Pozoroval stojaci západne od veže vidí jej vrchol pod výškovým uhlom 45 stupňov. Potom, čo sa posunie o 50 metrov na juh, vidí jej vrchol pod výškovým uhlom 30 stupňov. Ako vysoká je veža?
Správna odpoveď:

Tipy na súvisiace online kalkulačky
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
geometriaalgebraaritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Pozorovateľ 4
 Pozorovateľ vidí pätu veže vysokej 96 metrov pod hĺbkovým uhlom 30 stupňov a 10 minút a vrchol veže pod hĺbkovým uhlom 20 stupňov a 50 minút. Ako vysoko je pozorovateľ nad horizontálnou rovinou, na ktorej stojí veža?
Pozorovateľ vidí pätu veže vysokej 96 metrov pod hĺbkovým uhlom 30 stupňov a 10 minút a vrchol veže pod hĺbkovým uhlom 20 stupňov a 50 minút. Ako vysoko je pozorovateľ nad horizontálnou rovinou, na ktorej stojí veža? - TV tower
 Vypočítajte výšku televíznej veže, ak pozorovateľ, ktorý stojí 430 m od päty veže vidí vrchol pod výškovým uhlom 23°?
Vypočítajte výšku televíznej veže, ak pozorovateľ, ktorý stojí 430 m od päty veže vidí vrchol pod výškovým uhlom 23°? - Vrchol 3
 Vrchol eiffelovej veži vidíme zo vzdialenosti 600 metrov pod uhlom 30 stupňov. Určte výšku veže.
Vrchol eiffelovej veži vidíme zo vzdialenosti 600 metrov pod uhlom 30 stupňov. Určte výšku veže. - Pozorovateľ - uhly
 Pozorovateľ vidí lietadlo pod výškovým uhlom 35° (uhol od vodorovnej roviny). V tej chvíli lietadlo hlási výšku 4 km. Ako ďaleko od pozorovateľa je miesto, nad ktorým lietadlo letí. Zaokrúhli na stovky metrov.
Pozorovateľ vidí lietadlo pod výškovým uhlom 35° (uhol od vodorovnej roviny). V tej chvíli lietadlo hlási výšku 4 km. Ako ďaleko od pozorovateľa je miesto, nad ktorým lietadlo letí. Zaokrúhli na stovky metrov. - Vzducholoď - triangulácia
 Vzducholoď je vo výške x nad zemou. Pavol ju sleduje z miesta A pod výškovým uhlom 18 stupňov 26 minút. V tej istej chvíli ju vidí Peter z malého lietadla, ktoré práve prelieta nad Pavlom vo výške 150m. Peter vidí vzducholoď pod výškovým uhlom 11 stupňov
Vzducholoď je vo výške x nad zemou. Pavol ju sleduje z miesta A pod výškovým uhlom 18 stupňov 26 minút. V tej istej chvíli ju vidí Peter z malého lietadla, ktoré práve prelieta nad Pavlom vo výške 150m. Peter vidí vzducholoď pod výškovým uhlom 11 stupňov - Z okna 2
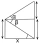 Z okna ležiaceho 8 m nad horizontálnou rovinou vidíme vrchol veže vo výškovom uhle 53 stupňov 20 minút, jej pätu v hĺbkovom uhle 14 stupňov 15 minút. Aká vysoká je veža?
Z okna ležiaceho 8 m nad horizontálnou rovinou vidíme vrchol veže vo výškovom uhle 53 stupňov 20 minút, jej pätu v hĺbkovom uhle 14 stupňov 15 minút. Aká vysoká je veža? - Vysoká veža
 Z veže 15 metrov vysokej a od rieky 30 metrov vzdialenej sa javila šírka rieky v uhle 15°. Aká široká je rieka v tomto mieste?
Z veže 15 metrov vysokej a od rieky 30 metrov vzdialenej sa javila šírka rieky v uhle 15°. Aká široká je rieka v tomto mieste?
