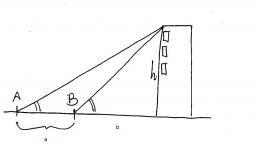
Angles of elevation

From points A and B on level ground, the angles of elevation of the top of a building are 25° and 37° respectively. If |AB| = 57m, calculate, to the nearest meter, the distances of the top of the building from A and B if they are both on the same side of the building.

Result

h =  69.73 m
d1 =  165 m
d2 =  116 m

Solution:

a=57 m A=(25∘→rad)=(25⋅ π180 )=0.436332312999 B=(37∘→rad)=(37⋅ π180 )=0.645771823238  tan⁡A=ha+b tan⁡B=hb b=htan⁡B  atan⁡A+btan⁡A=h atan⁡A+htan⁡Btan⁡A=h  h=a⋅ tan⁡(A)1−tan⁡(A)/tan⁡(B)=57⋅ tan⁡(0.4363)1−tan⁡(0.4363)/tan⁡(0.6458)≐69.728=69.73  m a = 57 \ m \ \\ A = (25^\circ \rightarrow rad) = (25 \cdot \ \dfrac{ \pi }{ 180 } \ ) = 0.436332312999 \ \\ B = (37^\circ \rightarrow rad) = (37 \cdot \ \dfrac{ \pi }{ 180 } \ ) = 0.645771823238 \ \\ \ \\ \tan A = \dfrac{ h }{ a+b } \ \\ \tan B = \dfrac{ h }{ b } \ \\ b = \dfrac{ h }{ \tan B } \ \\ \ \\ a \tan A + b \tan A = h \ \\ a \tan A + \dfrac{ h }{ \tan B } \tan A = h \ \\ \ \\ h = \dfrac{ a \cdot \ \tan(A) }{ 1 - \tan(A)/\tan(B) } = \dfrac{ 57 \cdot \ \tan(0.4363) }{ 1 - \tan(0.4363)/\tan(0.6458) } \doteq 69.728 = 69.73 \ \text { m }
b=htan⁡(B)=69.728tan⁡(0.6458)≐92.5348 m  d1=h2+(a+b)2=69.7282+(57+92.5348)2≐164.9938=165  m b = \dfrac{ h }{ \tan(B) } = \dfrac{ 69.728 }{ \tan(0.6458) } \doteq 92.5348 \ m \ \\ \ \\ d_{ 1 } = \sqrt{ h^2 + (a+b)^2 } = \sqrt{ 69.728^2 + (57+92.5348)^2 } \doteq 164.9938 = 165 \ \text { m }
d2=h2+b2=69.7282+92.53482≐115.8662=116  m d_{ 2 } = \sqrt{ h^2 + b^2 } = \sqrt{ 69.728^2 + 92.5348^2 } \doteq 115.8662 = 116 \ \text { m }

Try another example






Leave us a comment of this math problem and its solution (i.e. if it is still somewhat unclear...):

Showing 0 comments:
1st comment
Be the first to comment!
avatar




Following knowledge from mathematics are needed to solve this word math problem:

See also our right triangle calculator. See also our trigonometric triangle calculator. Try conversion angle units angle degrees, minutes, seconds, radians, grads.

Next similar math problems:

  1. Depth angles
    hrad At the top of the mountain stands a castle, which has a tower 30 meters high. We see the crossroad in the valley from the top of the tower and heel at depth angles of 32° 50 'and 30° 10'. How high is the top of the mountain above the crossroad
  2. Hole's angles
    Trapezium2-300x199 I am trying to find an angle. The top of the hole is .625” and the bottom of the hole is .532”. The hole depth is .250” what is the angle of the hole (and what is the formula)?
  3. Triangle P2
    1right_triangle Can triangle have two right angles?
  4. Angles
    triangle_1111_1 In the triangle ABC, the ratio of angles is: a:b = 4: 5. The angle c is 36°. How big are the angles a, b?
  5. How far
    lighthouse_1 From the top of a lighthouse 145 ft above sea level, the angle of depression of a boat 29°. How far is the boat from the lighthouse?
  6. Tree
    strom How tall is the tree that observed in the visual angle of 52°? If I stand 5 m from the tree and eyes are two meters above the ground.
  7. Maple
    tree_javor Maple peak is visible from a distance 3 m from the trunk from a height of 1.8 m at angle 62°. Determine the height of the maple.
  8. Depth angle
    cliff From a cliff of 150 meters high, we can see the ship at a depth angle of 9° at sea. How far is the ship from the cliff?
  9. Theorem prove
    thales_1 We want to prove the sentence: If the natural number n is divisible by six, then n is divisible by three. From what assumption we started?
  10. Building
    building The building I focused at an angle 30°. When I moved 5 m building I focused at an angle 45°. What is the height of the building?
  11. If the
    tan If the tangent of an angle of a right angled triangle is 0.8. Then its longest side is. .. .
  12. Reflector
    lamp Circular reflector throws light cone with a vertex angle 49° and is on 33 m height tower. The axis of the light beam has with the axis of the tower angle 30°. What is the maximum length of the illuminated horizontal plane?
  13. High wall
    mur I have a wall 2m high. I need a 15 degree angle (upward) to second wall 4 meters away. How high must the second wall?
  14. Reference angle
    anglemeter Find the reference angle of each angle:
  15. Descent of road
    znacka_klesanie Road sign informs the gradient is 10.3%. Calculate the angle which average decreases.
  16. Map - climb
    Lanovka_na_skalnate_pleso On the map of High Tatras in scale 1:11000 are cable car stations in the Tatranska Lomnica and in the Skalnate Pleso with distance 354.6 mm. Altitude of this stations are 949 m and 1760 m. What is average angle of climb of this cable car track?
  17. Effective and mean voltage
    serial-parallel A voltage divider consisting of resistors R1 = 103000 Ω and R2 = 197000 Ω is connected to the ideal sine wave voltage source, R2 is connected to a voltmeter which measures the mean voltage and has an internal resistance R3 = 200300 Ω, the measured value is