Vrchol budovy
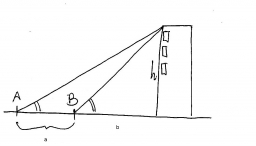
Z bodov A a B na rovnom povrchu sú uhly pozorovania vrcholu budovy 25° a 37°. Ak | AB | = 57 m, vypočítajte s presnosťou na najbližší meter vzdialenosti hornej časti budovy od A a B, ak sú obidve na tej istej strane budovy.
Správna odpoveď:
Tipy na súvisiace online kalkulačky
Chcete premeniť jednotku dĺžky?
Chcete zaokrúhliť číslo?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Chcete zaokrúhliť číslo?
Pozrite aj našu kalkulačku pravouhlého trojuholníka.
Pozrite aj našu trigonometrickú trojuholníkovu kalkulačku.
Vyskúšajte si prevody jednotiek uhlov uhlové stupne, minúty, sekundy, radiány.
Na vyriešenie tejto úlohy sú potrebné tieto znalosti z matematiky:
aritmetikaplanimetriagoniometria a trigonometriaJednotky fyzikálnych veličínÚroveň náročnosti úlohy
Súvisiace a podobné príklady:
- Rádiova anténa
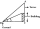 Avanti sa snaží nájsť výšku rádiovej antény na streche miestnej budovy. Stojí vo vodorovnej vzdialenosti 21 metrov od budovy. Uhol elevácie od jej očí k streche (bod A) je 42° a uhol elevácie od jej očí k vrcholu antény (bod B) je 51°. Ak sú jej oči 1,54
Avanti sa snaží nájsť výšku rádiovej antény na streche miestnej budovy. Stojí vo vodorovnej vzdialenosti 21 metrov od budovy. Uhol elevácie od jej očí k streche (bod A) je 42° a uhol elevácie od jej očí k vrcholu antény (bod B) je 51°. Ak sú jej oči 1,54 - Susedné uhly 3
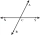 Uhly alfa a beta sú susedné . Vypočítajte veľkosť uhla beta ak alfa sa rovná 57°.
Uhly alfa a beta sú susedné . Vypočítajte veľkosť uhla beta ak alfa sa rovná 57°. - ABCD kosoštvorec
 ABCD je kosoštvorec so stranami 10,5 cm. Ak je dĺžka uhlopriečky AC = 15,8 cm, použite kosínusový vzorec. a. vypočítajte dĺžku uhlopriečky BD s presnosťou na najbližší cm b. uhly kosoštvorca s presnosťou na najbližší stupeň.
ABCD je kosoštvorec so stranami 10,5 cm. Ak je dĺžka uhlopriečky AC = 15,8 cm, použite kosínusový vzorec. a. vypočítajte dĺžku uhlopriečky BD s presnosťou na najbližší cm b. uhly kosoštvorca s presnosťou na najbližší stupeň. - Uhly lichobežníka
 V lichobežníku ABCD (AB CD) je α = 57°, γ = 4β. Vypočítajte veľkosť všetkých vnútorných uhlov.
V lichobežníku ABCD (AB CD) je α = 57°, γ = 4β. Vypočítajte veľkosť všetkých vnútorných uhlov. - Tieň 2
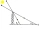 Tieň veže stojacej na rovnom povrchu je o 40 m dlhší, keď je výška Slnka 30°, ako keď je 60°. Nájdite výšku veže.
Tieň veže stojacej na rovnom povrchu je o 40 m dlhší, keď je výška Slnka 30°, ako keď je 60°. Nájdite výšku veže. - Pozorovací uhol
 Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A.
Z bodu A na zemi je pozorovací uhol vrcholu 20 m vysokej budovy 45°. Na vrchole budovy je vztýčená vlajka a pozorovací uhol vrcholu vlajkovej tyče od A je 60°. Nájdite dĺžku vlajkovej tyče a vzdialenosť budovy od bodu A. - Uhly
 V trojuholníku má jeden vonkajší uhol veľkosť 157°18' a jeden vnútorný uhol 111°42'. Vypočítajte ostatné vnútorné uhly trojuholníka.
V trojuholníku má jeden vonkajší uhol veľkosť 157°18' a jeden vnútorný uhol 111°42'. Vypočítajte ostatné vnútorné uhly trojuholníka.
