A ship
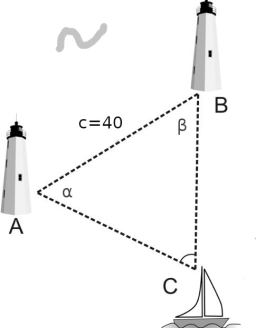
A ship has been spotted by two lighthouses, A and B, as shown in the figure. What is the distance from the ship to Lighthouse A to the nearest tenth? Figure - the distance between lighthouses A and B is 40 nautical miles. From A is seen in view angle 57° and from B at 64° angle.
Correct answer:
Showing 1 comment:
Dr. Math
Solution:
To find the distance from the ship to Lighthouse A, we can use the Law of Sines. The given information is:
- The distance between Lighthouse A and Lighthouse B is 40 nautical miles.
- The angle at Lighthouse A is 57° .
- The angle at Lighthouse B is 64° .
Step 1: Find the angle at the ship.
The sum of angles in a triangle is 180° . Therefore, the angle at the ship ( C ) is:
Step 2: Use the Law of Sines to find the distance from the ship to Lighthouse A.
The Law of Sines states:
Here:
- a is the distance from the ship to Lighthouse B,
- b is the distance from the ship to Lighthouse A (the value we are solving for),
- c = 40 nautical miles (the distance between Lighthouse A and Lighthouse B),
- A = 57° (the angle at Lighthouse A),
- B = 64° (the angle at Lighthouse B),
- C = 59° (the angle at the ship).
Using the Law of Sines:
Solve for b :
Final Answer:
The distance from the ship to Lighthouse A is approximately:
To find the distance from the ship to Lighthouse A, we can use the Law of Sines. The given information is:
- The distance between Lighthouse A and Lighthouse B is 40 nautical miles.
- The angle at Lighthouse A is 57° .
- The angle at Lighthouse B is 64° .
Step 1: Find the angle at the ship.
The sum of angles in a triangle is 180° . Therefore, the angle at the ship ( C ) is:
C = 180° - 57° - 64° = 59°
Step 2: Use the Law of Sines to find the distance from the ship to Lighthouse A.
The Law of Sines states:
asin A = bsin B = csin C
Here:
- a is the distance from the ship to Lighthouse B,
- b is the distance from the ship to Lighthouse A (the value we are solving for),
- c = 40 nautical miles (the distance between Lighthouse A and Lighthouse B),
- A = 57° (the angle at Lighthouse A),
- B = 64° (the angle at Lighthouse B),
- C = 59° (the angle at the ship).
Using the Law of Sines:
bsin 64° = 40sin 59°
Solve for b :
b = 40 · sin 64°sin 59°
b = ≈ 41.9
Final Answer:
The distance from the ship to Lighthouse A is approximately:
41.9 nautical miles
Tips for related online calculators
Check out our ratio calculator.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
Do you want to convert length units?
See also our trigonometric triangle calculator.
Try conversion angle units angle degrees, minutes, seconds, radians, grads.
You need to know the following knowledge to solve this word math problem:
planimetricsbasic operations and conceptsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Tower's view
From the church tower's view at 65 m, the top of the house can be seen at a depth angle of alpha = 45° and its bottom at a depth angle of beta = 58°. Calculate the house's height and its distance from the church. - Chimney - view angle
From a distance of 36 meters from the chimney base, its top can be seen at an angle of 53°. Calculate the chimney height and the result round to whole decimeters. - A hiker
A hiker plans to hike up one side of a mountain and down the other side of points a mountain, each side of the mountain formed by a straight line. The angle of elevation at the starting point is 42.4 degrees, and the angle of elevation at the end is 48.3 - An angle of depression
The lighthouse sees a ship at an angle of depression of 25°. The observer from the lighthouse is 82 m above sea level. How far is the ship from the top of the lighthouse?
- Consider 6
Consider the following word problem: The temperature readings for 20 days at 1 AM at a local ski resort were recorded as follows: 9° 27° −4° 1° 5° 14° 6° 28° −2° 16° 30° 4° 20° 30° −5° 15° −7° 25° −1° 5° What was the average of the recorded temperatures f - Bearing - navigation
A ship travels 84 km on a bearing of 17° and then travels on a bearing of 107° for 135 km. Find the distance of the end of the trip from the starting point to the nearest kilometer. - Measurements 8129
The plane flies at an altitude of 22.5 km to the observatory. At the time of the first measurement, it was seen at an elevation angle of 28° and during the second measurement at an elevation angle of 50°. Calculate the distance it flies between these two
