Coordinates of square vertices
The ABCD square has the center S [−3, −2] and the vertex A [1, −3]. Find the coordinates of the other vertices of the square.
Correct answer:
Tips for related online calculators
Line slope calculator is helpful for basic calculations in analytic geometry. The coordinates of two points in the plane calculate slope, normal and parametric line equation(s), slope, directional angle, direction vector, the length of the segment, intersections of the coordinate axes, etc.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
You need to know the following knowledge to solve this word math problem:
We encourage you to watch this tutorial video on this math problem: video1
Related math problems and questions:
- Center
In the ABC triangle is point D[1,-2,6], which is the center of the |BC|, and point G[8,1,-3], which is the center of gravity of the triangle. Find the coordinates of the vertex A[x,y,z]. - Calculate 7
Calculate the height of the trapezoid ABCD, where coordinates of vertices are: A[2, 1], B[8, 5], C[5, 5] and D[2, 3] - Coordinates hexagon
The regular hexagon ABCDEF is given. Point A has coordinates [1; 3], and point D has coordinates [4; 7]. Calculate the sum of the coordinates of the center of its described circle. - Chord BC
A circle k has the center at the point S = [0; 0]. Point A = [40; 30] lies on the circle k. How long is the chord BC if the center P of this chord has the coordinates: [- 14; 0]? - Intersection 3486
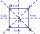There is a point A [-2; -4] in the rectangular coordinate system and a point S [0; -2]. Determine the coordinates of points B, C, and D so that ABCD is a square and S is the intersection of their diagonals. - Segment
Calculate the segment AB's length if the coordinates of the end vertices are A[10, -4] and B[5, 5]. - Intersections 25141
The quadratic function has the formula y = x²-2x-3. Sketch a graph of this function. Find the intersections with the axes. Find the vertex coordinates. - Calculate 8
Calculate the coordinates of point B axially symmetrical with point A[-1, -3] along a straight line p : x + y - 2 = 0. - Determine Determine which type of quadrilateral ABCD is and find its perimeter if you know coordinates of vertices: A/2,4 /, B / -2,1 /, C / -2, -2 /, D/2, -5 /.
- The triangle
The triangle is given by three vertices: A [0.0] B [-4.2] C [-6.0] Calculate V (intersection of heights), T (center of gravity), O - center of a circle circumscribed - Midpoint of segment
Point A has coordinates [4; -11] and the midpoint of the segment AB is the point [17; -7]. What are the coordinates of point B? - Circle
From the equation of a circle: 2x² +2y² +20x -20y +68 = 0 Calculate the coordinates of the center of the circle S[x0, y0] and radius of the circle r. - Coordinates of the intersection of the diagonals
In the rectangular coordinate system, a rectangle ABCD is drawn. These coordinates determine the vertices of the rectangle. A = (2.2) B = (8.2) C = (8.6) D = (2.6) Find the coordinates of the intersection of the diagonals of the ABCD rectangle. - Center
Calculate the coordinates of the center of gravity T [x, y] of triangle ABC; A[11,4] B[13,-7] C[-17,-18]. - Center of gravity
The mass points are distributed in space as follows - specify by coordinates and weight. Find the center of gravity of the mass points system: A1 [1; -20; 3] m1 = 46 kg A2 [-20; 2; 9] m2 = 81 kg A3 [9 - Isosceles triangle
In an isosceles triangle ABC with base AB; A [3,4]; B [1,6] and the vertex C lies on the line 5x - 6y - 16 = 0. Calculate the coordinates of vertex C. - Square side
Calculate length of side square ABCD with vertex A[0, 0] if diagonal BD lies on line p: -4x -5 =0.
