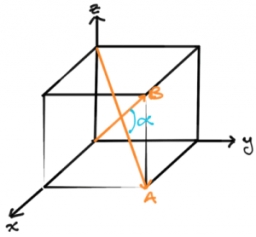
Angle of the body diagonals
Using the vector dot product calculate the angle of the body diagonals of the cube.
Correct answer:
Tips for related online calculators
Our vector sum calculator can add two vectors given by their magnitudes and by included angle.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
See also our right triangle calculator.
See also our trigonometric triangle calculator.
You need to know the following knowledge to solve this word math problem:
geometryarithmeticsolid geometryplanimetricsgoniometry and trigonometryUnits of physical quantitiesGrade of the word problem
Related math problems and questions:
- Scalar dot product
Calculate u.v if |u| = 5, |v| = 2 and when the angle between the vectors u, v is: a) 60° b) 45° c) 120° - Calculate 83044
The cube comprises 64 small cubes, each with an edge length of 15 mm. Calculate the wall length and body diagonals. - Diagonals 7084
Calculate the lengths of the wall and body diagonals of the cube with an edge length of 10 cm. - Scalar product
Calculate the scalar product of two vectors: (2.5) (-1, -4) - Cube diagonals The cube has a wall area of 81 cm square. Calculate the length of its edge, wall, and body diagonal.
- Calculate 32133
The cube has an area of 486 dm². Calculate the length of its side, its volume, the length of the body, and wall diagonals. - Calculate cuboid
Given cuboid ABCDEFGH. We know that |AB| = 1 cm, |BC| = 2 cm, |AE| = 3 cm. Calculate in degrees the angle size formed by the lines BG and FH .
